Calculating and plotting the relative vorticity

Vorticity, the microscopic measure of rotation in a fluid, is a vector field defined as the curl of velocity (James R. Holton, Gregory J. Hakim, An Introduction to Dynamic Meteorology, 2013, Elsevier : Academic Press p95-125). In this recipe, we will be calculating and plotting the relative vorticity from the wind components.

1. Import cf-python and cf-plot:

import cfplot as cfp

import cf

2. Read the field constructs:

f = cf.read("~/recipes/ERA5_monthly_averaged_pressure_levels.nc")
print(f)

[<CF Field: divergence_of_wind(long_name=time(3), long_name=expver(2), long_name=latitude(721), long_name=longitude(1440)) s**-1>,
 <CF Field: eastward_wind(long_name=time(3), long_name=expver(2), long_name=latitude(721), long_name=longitude(1440)) m s**-1>,
 <CF Field: northward_wind(long_name=time(3), long_name=expver(2), long_name=latitude(721), long_name=longitude(1440)) m s**-1>]

3. Select wind components and look at their contents:

u = f.select_field("eastward_wind")
print(u)

Field: eastward_wind (ncvar%u)
------------------------------
Data            : eastward_wind(long_name=time(3), long_name=expver(2), long_name=latitude(721), long_name=longitude(1440)) m s**-1
Dimension coords: long_name=time(3) = [2023-01-01 00:00:00, 2023-02-01 00:00:00, 2023-03-01 00:00:00] gregorian
                : long_name=expver(2) = [1, 5]
                : long_name=latitude(721) = [90.0, ..., -90.0] degrees_north
                : long_name=longitude(1440) = [0.0, ..., 359.75] degrees_east

v = f.select_field("northward_wind")
print(v)

Field: northward_wind (ncvar%v)
-------------------------------
Data            : northward_wind(long_name=time(3), long_name=expver(2), long_name=latitude(721), long_name=longitude(1440)) m s**-1
Dimension coords: long_name=time(3) = [2023-01-01 00:00:00, 2023-02-01 00:00:00, 2023-03-01 00:00:00] gregorian
                : long_name=expver(2) = [1, 5]
                : long_name=latitude(721) = [90.0, ..., -90.0] degrees_north
                : long_name=longitude(1440) = [0.0, ..., 359.75] degrees_east

4. Create a date-time object for the required time period:

jan_2023 = cf.year(2023) & cf.month(1)

5. The relative vorticity is calculated using cf.curl_xy and plotted using cfplot.con. The with cf.relaxed_identities(True) context manager statement prevents the curl opereration broadcasting across the two expver dimensions because it can’t be certain that they are the same as they lack the standardised metadata. Setting cf.relaxed_identities(True) allows the long_name to be treated as standardised metadata. Since the horizontal coordinates are latitude and longitude, the cf.curl_xy function automatically accounts for the Earth’s spherical geometry when calculating the spatial derivatives in the horizontal directions, and for this it requires the Earth’s radius. In this case the radius is not stored in the wind fields, so must be provided by setting radius="earth" keyword parameter. While plotting, the relative vorticity is subspaced for January 2023 and one of the experiment versions using the dictionary unpacking operator (**) as there is an equal to sign in the identifier ("long_name=expver"):

with cf.relaxed_identities(True):
    rv = cf.curl_xy(u, v, radius="earth")

cfp.con(
    rv.subspace(T=jan_2023, **{"long_name=expver": 1}),
    lines=False,
    title="Relative Vorticity",
)

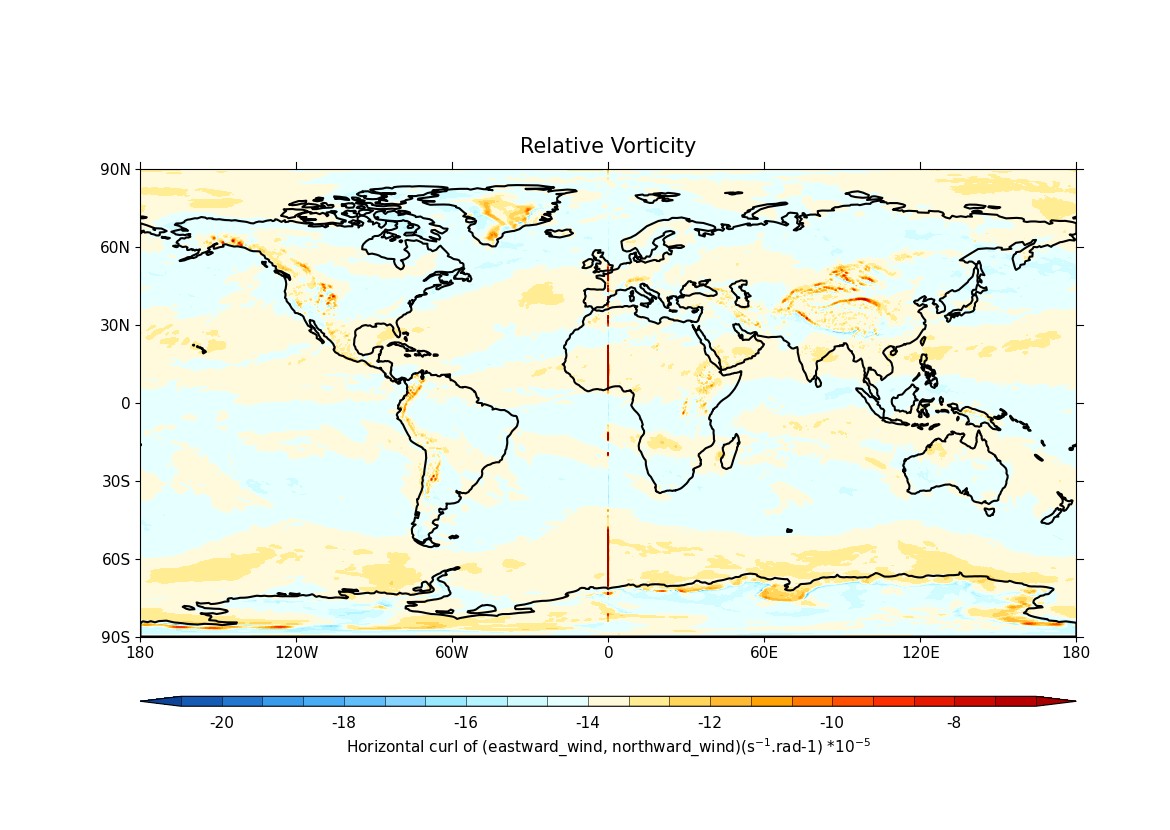
6. Although the X axis is cyclic, it is not recognised as such, owing to the fact that the longitude coordinate bounds are missing. This results in discontinuities in the calculated vorticity field on the plot at the wrap-around location of 0 degrees east. The cyclicity could either be set on the field itself or just in the curl command by setting 'x_wrap=True' while calculating the relative vorticity. Setting rv.units = "s-1", ensures that the units of the relative vorticity field are consistent with the calculation and the physical interpretation of the quantity:

print(v.coordinate("X").has_bounds())

False

with cf.relaxed_identities(True):
    rv = cf.curl_xy(u, v, x_wrap=True, radius="earth")

rv.units = "s-1"
print(rv)

Field: long_name=Horizontal curl of (eastward_wind, northward_wind) (ncvar%u)
-----------------------------------------------------------------------------
Data            : long_name=Horizontal curl of (eastward_wind, northward_wind)(long_name=time(3), long_name=expver(2), latitude(721), longitude(1440)) s-1
Dimension coords: long_name=time(3) = [2023-01-01 00:00:00, 2023-02-01 00:00:00, 2023-03-01 00:00:00] gregorian
                : long_name=expver(2) = [1, 5]
                : latitude(721) = [90.0, ..., -90.0] degrees_north
                : longitude(1440) = [0.0, ..., 359.75] degrees_east

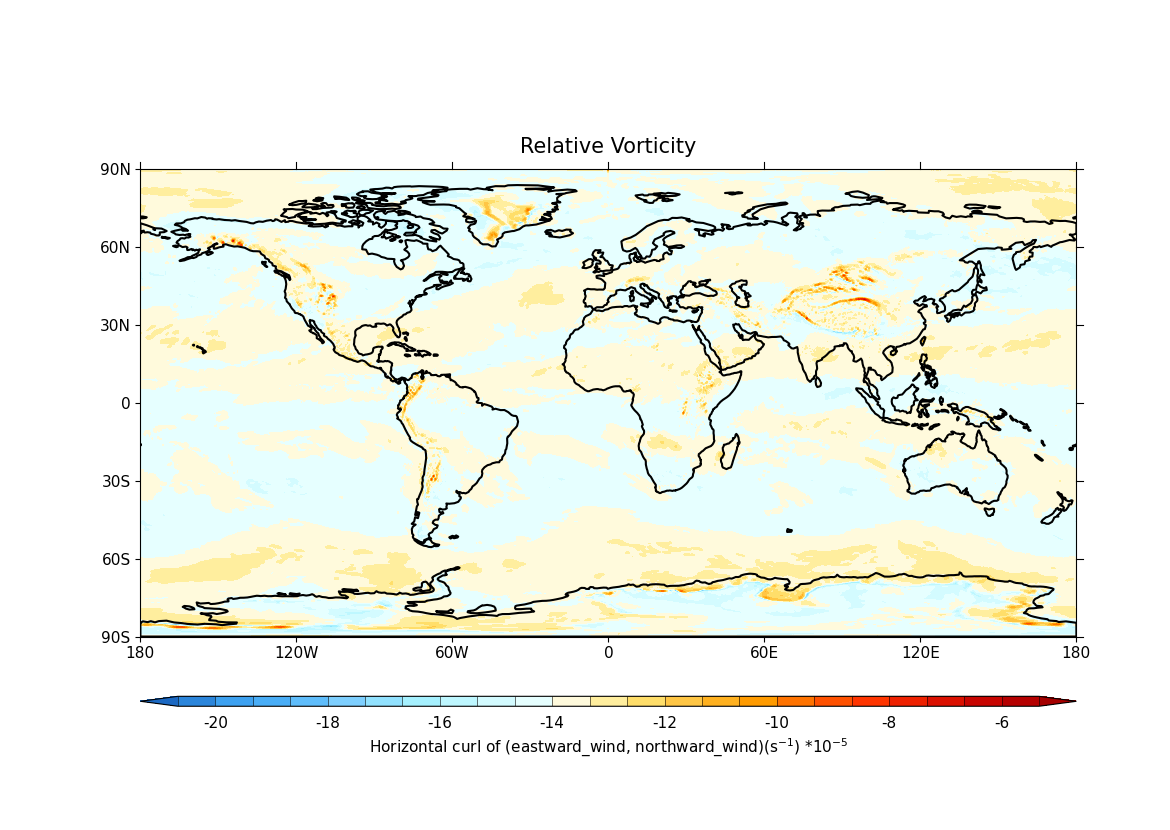
cfp.con(
    rv.subspace(T=jan_2023, **{"long_name=expver": 1}),
    lines=False,
    title="Relative Vorticity",
)