Calculating and plotting the global average temperature anomalies

In this recipe we will calculate and plot the global average temperature anomalies.

1. Import cf-python and cf-plot:

import cfplot as cfp

import cf

2. Read the field constructs:

f = cf.read("~/recipes/cru_ts4.06.1901.2021.tmp.dat.nc")
print(f)

[<CF Field: ncvar%stn(long_name=time(1452), long_name=latitude(360), long_name=longitude(720))>,
 <CF Field: long_name=near-surface temperature(long_name=time(1452), long_name=latitude(360), long_name=longitude(720)) degrees Celsius>]

3. Select near surface temperature by index and look at its contents:

temp = f[1]
print(temp)

Field: long_name=near-surface temperature (ncvar%tmp)
-----------------------------------------------------
Data            : long_name=near-surface temperature(long_name=time(1452), long_name=latitude(360), long_name=longitude(720)) degrees Celsius
Dimension coords: long_name=time(1452) = [1901-01-16 00:00:00, ..., 2021-12-16 00:00:00] gregorian
                : long_name=latitude(360) = [-89.75, ..., 89.75] degrees_north
                : long_name=longitude(720) = [-179.75, ..., 179.75] degrees_east

4. Select latitude and longitude dimensions by identities, with two different techniques:

lon = temp.coordinate("long_name=longitude")
lat = temp.coordinate("Y")

5. Print the description of near surface temperature to show properties of all constructs:

temp.dump()

-----------------------------------------------------
Field: long_name=near-surface temperature (ncvar%tmp)
-----------------------------------------------------
Conventions = 'CF-1.4'
_FillValue = 9.96921e+36
comment = 'Access to these data is available to any registered CEDA user.'
contact = 'support@ceda.ac.uk'
correlation_decay_distance = 1200.0
history = 'Fri 29 Apr 14:35:01 BST 2022 : User f098 : Program makegridsauto.for
           called by update.for'
institution = 'Data held at British Atmospheric Data Centre, RAL, UK.'
long_name = 'near-surface temperature'
missing_value = 9.96921e+36
references = 'Information on the data is available at
              http://badc.nerc.ac.uk/data/cru/'
source = 'Run ID = 2204291347. Data generated from:tmp.2204291209.dtb'
title = 'CRU TS4.06 Mean Temperature'
units = 'degrees Celsius'

Data(long_name=time(1452), long_name=latitude(360), long_name=longitude(720)) = [[[--, ..., --]]] degrees Celsius

Domain Axis: long_name=latitude(360)
Domain Axis: long_name=longitude(720)
Domain Axis: long_name=time(1452)

Dimension coordinate: long_name=time
    calendar = 'gregorian'
    long_name = 'time'
    units = 'days since 1900-1-1'
    Data(long_name=time(1452)) = [1901-01-16 00:00:00, ..., 2021-12-16 00:00:00] gregorian

Dimension coordinate: long_name=latitude
    long_name = 'latitude'
    units = 'degrees_north'
    Data(long_name=latitude(360)) = [-89.75, ..., 89.75] degrees_north

Dimension coordinate: long_name=longitude
    long_name = 'longitude'
    units = 'degrees_east'
    Data(long_name=longitude(720)) = [-179.75, ..., 179.75] degrees_east

6. Latitude and longitude dimension coordinate cell bounds are absent, which are created and set:

a = lat.create_bounds()
lat.set_bounds(a)
lat.dump()

Dimension coordinate: long_name=latitude
    long_name = 'latitude'
    units = 'degrees_north'
    Data(360) = [-89.75, ..., 89.75] degrees_north
    Bounds:units = 'degrees_north'
    Bounds:Data(360, 2) = [[-90.0, ..., 90.0]] degrees_north

b = lon.create_bounds()
lon.set_bounds(b)
lon.dump()

Dimension coordinate: long_name=longitude
    long_name = 'longitude'
    units = 'degrees_east'
    Data(720) = [-179.75, ..., 179.75] degrees_east
    Bounds:units = 'degrees_east'
    Bounds:Data(720, 2) = [[-180.0, ..., 180.0]] degrees_east

print(b.array)

[[-180.  -179.5]
 [-179.5 -179. ]
 [-179.  -178.5]
 ...
 [ 178.5  179. ]
 [ 179.   179.5]
 [ 179.5  180. ]]

7. Time dimension coordinate cell bounds are similarly created and set for cell sizes of one calendar month:

time = temp.coordinate("long_name=time")
c = time.create_bounds(cellsize=cf.M())
time.set_bounds(c)
time.dump()

Dimension coordinate: long_name=time
    calendar = 'gregorian'
    long_name = 'time'
    units = 'days since 1900-1-1'
    Data(1452) = [1901-01-16 00:00:00, ..., 2021-12-16 00:00:00] gregorian
    Bounds:calendar = 'gregorian'
    Bounds:units = 'days since 1900-1-1'
    Bounds:Data(1452, 2) = [[1901-01-01 00:00:00, ..., 2022-01-01 00:00:00]] gregorian

8. Calculate the area weighted mean surface temperature for each time using the collapse method:

global_avg = temp.collapse("area: mean", weights=True)

9. Calculate the annual global mean surface temperature:

annual_global_avg = global_avg.collapse("T: mean", group=cf.Y())

10. The temperature values are averaged for the climatological period of 1961-1990 by defining a subspace within these years using cf.wi query instance over subspace and doing a statistical collapse with the collapse method:

annual_global_avg_61_90 = annual_global_avg.subspace(
    T=cf.year(cf.wi(1961, 1990))
)
print(annual_global_avg_61_90)

Field: long_name=near-surface temperature (ncvar%tmp)
-----------------------------------------------------
Data            : long_name=near-surface temperature(long_name=time(30), long_name=latitude(1), long_name=longitude(1)) degrees Celsius
Cell methods    : area: mean long_name=time(30): mean
Dimension coords: long_name=time(30) = [1961-07-02 12:00:00, ..., 1990-07-02 12:00:00] gregorian
                : long_name=latitude(1) = [0.0] degrees_north
                : long_name=longitude(1) = [0.0] degrees_east

temp_clim = annual_global_avg_61_90.collapse("T: mean")
print(temp_clim)

Field: long_name=near-surface temperature (ncvar%tmp)
-----------------------------------------------------
Data            : long_name=near-surface temperature(long_name=time(1), long_name=latitude(1), long_name=longitude(1)) degrees Celsius
Cell methods    : area: mean long_name=time(1): mean
Dimension coords: long_name=time(1) = [1976-01-01 12:00:00] gregorian
                : long_name=latitude(1) = [0.0] degrees_north
                : long_name=longitude(1) = [0.0] degrees_east

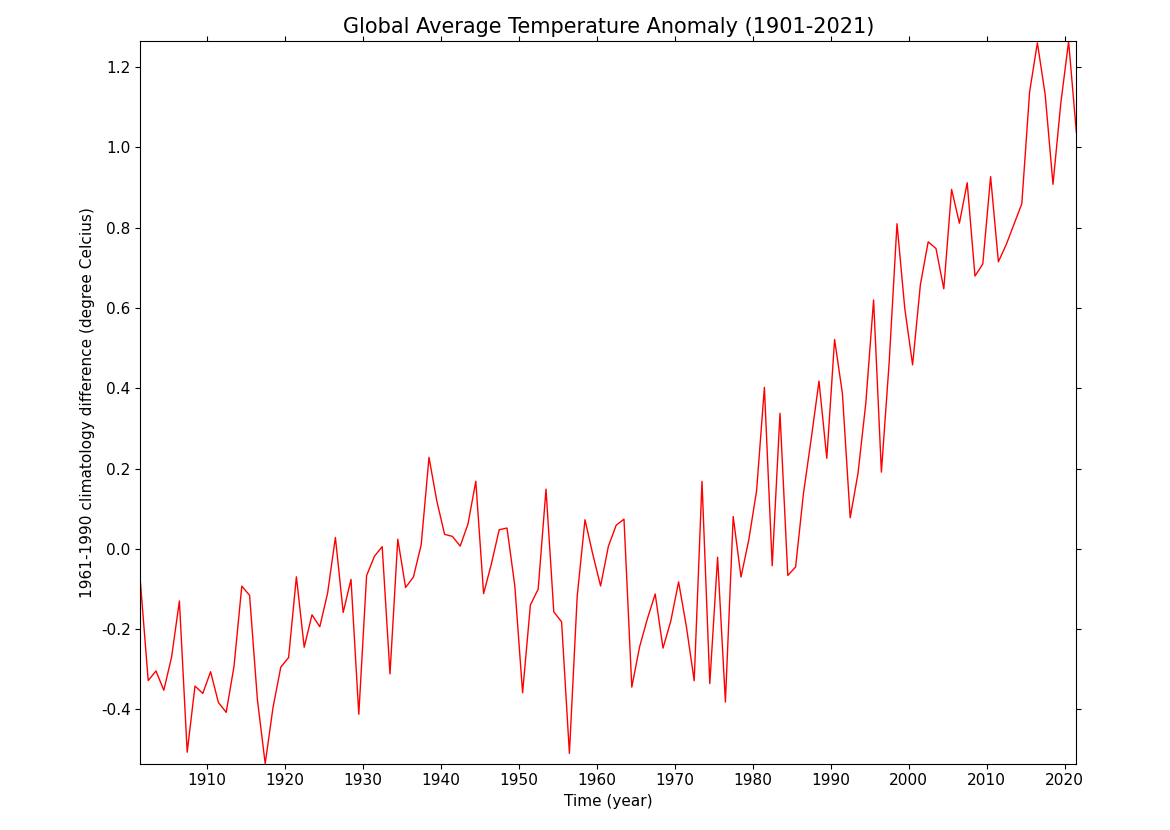
11. The temperature anomaly is then calculated by subtracting these climatological temperature values from the annual global average temperatures and plotted:

temp_anomaly = annual_global_avg - temp_clim
cfp.lineplot(
    temp_anomaly,
    color="red",
    title="Global Average Temperature Anomaly (1901-2021)",
    ylabel="1961-1990 climatology difference ",
    yunits="degree Celcius",
)