Tutorial

---

Version 3.2.0 for version 1.8 of the CF conventions.

All of the Python code in this tutorial is available in an executable script (download, 36kB).

Important

This version of cf is for Python 3 only and there are incompatible differences between versions 2.x and 3.x of cf.

Scripts written for version 2.x but running under version 3.x should either work as expected, or provide informative error messages on the new API usage. However, it is advised that the outputs of older scripts are checked when running with Python 3 versions of the cf library.

For version 2.x documentation, see the older releases page.

Sample datasets

This tutorial uses a number of small sample datasets, all of which can be found in the zip file cf_tutorial_files.zip (download, 164kB):

Unpack the sample datasets.

$ unzip -q cf_tutorial_files.zip
$ ls -1
air_temperature.nc
cf_tutorial_files.zip
contiguous.nc
external.nc
file2.nc
file.nc
gathered.nc
parent.nc
precipitation_flux.nc
timeseries.nc
umfile.pp
vertical.nc
wind_components.nc

The tutorial examples assume that the Python session is being run from the directory that contains the zip file and its unpacked contents, and no other files.

The tutorial files may be also found in the downloads directory of the on-line code repository.

---

Import

The cf package is imported as follows:

Import the cf package.

>>> import cf

CF version

The version of the CF conventions and the CF data model being used may be found with the cf.CF function:

Retrieve the version of the CF conventions.

>>> cf.CF()
'1.8'

This indicates which version of the CF conventions are represented by this release of the cf package, and therefore the version can not be changed.

Note, however, that datasets of different CF versions may be read from, or written to netCDF.

---

Field construct

The central construct (i.e. element) to CF is the field construct. The field construct, that corresponds to a CF-netCDF data variable, includes all of the metadata to describe it:

• descriptive properties that apply to field construct as a whole (e.g. the standard name),

• a data array, and

• “metadata constructs” that describe the locations of each cell of the data array, and the physical nature of each cell’s datum.

A field construct is stored in a cf.Field instance, and henceforth the phrase “field construct” will be assumed to mean “cf.Field instance”.

---

Reading field constructs from datasets

The cf.read function reads files from disk, or from an OPeNDAP URLs 1, and returns the contents in a cf.FieldList instance that contains zero or more cf.Field instances, each of which represents a field construct. Henceforth, the phrase “field list” will be assumed to mean a cf.FieldList instance.

A field list is very much like a Python list, with the addition of extra methods that operate on its field construct elements.

The following file types can be read:

• All formats of netCDF3 and netCDF4 files (including CFA-netCDF files) can be read, containing datasets for any version of CF up to and including CF-1.8.

• Files in CDL format, with or without the data array values.

• PP and UM fields files, whose contents are mapped into field constructs.

• A future release of cf will include support for netCDF4 files containing data organised in hierarchical groups, but this is not available in version 3.2.0 (even though it is allowed in CF-1.8).

For example, to read the file file.nc (found in the sample datasets), which contains two field constructs:

Read file.nc and show that the result is a two-element field list.

>>> x = cf.read('file.nc')
>>> type(x)
<class 'cf.fieldlist.FieldList'>
>>> len(x)
2

Descriptive properties are always read into memory, but lazy loading is employed for all data arrays, which means that no data is read into memory until the data is required for inspection or to modify the array contents. This maximises the number of field constructs that may be read within a session, and makes the read operation fast.

Multiple files may be read in one command using UNIX wild card characters, or a sequence of file names (each element of which may also contain wild cards). Shell environment variables are also permitted.

Read the ten sample netCDF files, noting that they contain more than ten field constructs.

>>> y = cf.read('*.nc')
>>> len(y)
14

Read two particular files, noting that they contain more than two field constructs.

>>> z = cf.read(['file.nc', 'precipitation_flux.nc'])
>>> len(z)
3

All of the datasets in one more directories may also be read by replacing any file name with a directory name. An attempt will be made to read all files in the directory, which will result in an error if any have a non-supported format. Non-supported files may be ignored with the ignore_read_error keyword.

Read all of the files in the current working directory.

>>> y = cf.read('$PWD')  # Raises Exception
Traceback (most recent call last):
    ...
Exception: Can't determine format of file cf_tutorial_files.zip
>>> y = cf.read('$PWD', ignore_read_error=True)
>>> len(y)
15

In all cases, the default behaviour is to aggregate the contents of all input datasets into as few field constructs as possible, and it is these aggregated field constructs are returned by cf.read. See the section on aggregation for full details.

The cf.read function has optional parameters to

• allow the user to provide files that contain external variables;

• request extra field constructs to be created from “metadata” netCDF variables, i.e. those that are referenced from CF-netCDF data variables, but which are not regarded by default as data variables in their own right;

• display information and warnings about the mapping of the netCDF file contents to CF data model constructs;

• remove from, or include, size one dimensions on the field constructs’ data;

• configure the field construct aggregation process;

• configure the reading of directories to allow sub-directories to be read recursively, and to allow directories which resolve to symbolic links; and

• configure parameters for reading PP and UM fields files.

CF-compliance

If the dataset is partially CF-compliant to the extent that it is not possible to unambiguously map an element of the netCDF dataset to an element of the CF data model, then a field construct is still returned, but may be incomplete. This is so that datasets which are partially conformant may nonetheless be modified in memory and written to new datasets. Such “structural” non-compliance would occur, for example, if the “coordinates” attribute of a CF-netCDF data variable refers to another variable that does not exist, or refers to a variable that spans a netCDF dimension that does not apply to the data variable. Other types of non-compliance are not checked, such whether or not controlled vocabularies have been adhered to. The structural compliance of the dataset may be checked with the dataset_compliance method of the field construct, as well as optionally displayed when the dataset is read.

---

Inspection

The contents of a field construct may be inspected at three different levels of detail.

Minimal detail

The built-in repr function, invoked on a variable by calling that variable alone at the interpreter prompt, returns a short, one-line description:

Inspect the contents of the two field constructs from the dataset and create a Python variable for each of them.

>>> x = cf.read('file.nc')
>>> x
[<CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>]
>>> q = x[0]
>>> t = x[1]
>>> q
<CF Field: specific_humidity(latitude(5), longitude(8)) 1>

This gives the identity of the field construct (e.g. “specific_humidity”), the identities and sizes of the dimensions spanned by the data array (“latitude” and “longitude” with sizes 5 and 8 respectively) and the units of the data (“1”, i.e. dimensionless).

Medium detail

The built-in str function, invoked by a print call on a field construct, returns similar information as the one-line output, along with short descriptions of the metadata constructs, which include the first and last values of their data arrays:

Inspect the contents of the two field constructs with medium detail.

>>> print(q)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(t)
Field: air_temperature (ncvar%ta)
---------------------------------
Data            : air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
Cell methods    : grid_latitude(10): grid_longitude(9): mean where land (interval: 0.1 degrees) time(1): maximum
Field ancils    : air_temperature standard_error(grid_latitude(10), grid_longitude(9)) = [[0.76, ..., 0.32]] K
Dimension coords: atmosphere_hybrid_height_coordinate(1) = [1.5]
                : grid_latitude(10) = [2.2, ..., -1.76] degrees
                : grid_longitude(9) = [-4.7, ..., -1.18] degrees
                : time(1) = [2019-01-01 00:00:00]
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[53.941, ..., 50.225]] degrees_N
                : longitude(grid_longitude(9), grid_latitude(10)) = [[2.004, ..., 8.156]] degrees_E
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., b'kappa']
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[2391.9657, ..., 2392.6009]] km2
Coord references: grid_mapping_name:rotated_latitude_longitude
                : standard_name:atmosphere_hybrid_height_coordinate
Domain ancils   : ncvar%a(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
                : ncvar%b(atmosphere_hybrid_height_coordinate(1)) = [20.0]
                : surface_altitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 270.0]] m

Note that time values are converted to date-times with the cftime package.

Full detail

The dump method of the field construct gives all properties of all constructs, including metadata constructs and their components, and shows the first and last values of all data arrays:

Inspect the contents of the two field constructs with full detail.

>>> q.dump()
----------------------------------
Field: specific_humidity (ncvar%q)
----------------------------------
Conventions = 'CF-1.7'
project = 'research'
standard_name = 'specific_humidity'
units = '1'

Data(latitude(5), longitude(8)) = [[0.003, ..., 0.032]] 1

Cell Method: area: mean

Domain Axis: latitude(5)
Domain Axis: longitude(8)
Domain Axis: time(1)

Dimension coordinate: latitude
    standard_name = 'latitude'
    units = 'degrees_north'
    Data(latitude(5)) = [-75.0, ..., 75.0] degrees_north
    Bounds:Data(latitude(5), 2) = [[-90.0, ..., 90.0]]

Dimension coordinate: longitude
    standard_name = 'longitude'
    units = 'degrees_east'
    Data(longitude(8)) = [22.5, ..., 337.5] degrees_east
    Bounds:Data(longitude(8), 2) = [[0.0, ..., 360.0]]

Dimension coordinate: time
    standard_name = 'time'
    units = 'days since 2018-12-01'
    Data(time(1)) = [2019-01-01 00:00:00]

>>> t.dump()
---------------------------------
Field: air_temperature (ncvar%ta)
---------------------------------
Conventions = 'CF-1.7'
project = 'research'
standard_name = 'air_temperature'
units = 'K'

Data(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) = [[[0.0, ..., 89.0]]] K

Cell Method: grid_latitude(10): grid_longitude(9): mean where land (interval: 0.1 degrees)
Cell Method: time(1): maximum

Field Ancillary: air_temperature standard_error
    standard_name = 'air_temperature standard_error'
    units = 'K'
    Data(grid_latitude(10), grid_longitude(9)) = [[0.76, ..., 0.32]] K

Domain Axis: atmosphere_hybrid_height_coordinate(1)
Domain Axis: grid_latitude(10)
Domain Axis: grid_longitude(9)
Domain Axis: time(1)

Dimension coordinate: atmosphere_hybrid_height_coordinate
    computed_standard_name = 'altitude'
    standard_name = 'atmosphere_hybrid_height_coordinate'
    Data(atmosphere_hybrid_height_coordinate(1)) = [1.5]
    Bounds:Data(atmosphere_hybrid_height_coordinate(1), 2) = [[1.0, 2.0]]

Dimension coordinate: grid_latitude
    standard_name = 'grid_latitude'
    units = 'degrees'
    Data(grid_latitude(10)) = [2.2, ..., -1.76] degrees
    Bounds:Data(grid_latitude(10), 2) = [[2.42, ..., -1.98]]

Dimension coordinate: grid_longitude
    standard_name = 'grid_longitude'
    units = 'degrees'
    Data(grid_longitude(9)) = [-4.7, ..., -1.18] degrees
    Bounds:Data(grid_longitude(9), 2) = [[-4.92, ..., -0.96]]

Dimension coordinate: time
    standard_name = 'time'
    units = 'days since 2018-12-01'
    Data(time(1)) = [2019-01-01 00:00:00]

Auxiliary coordinate: latitude
    standard_name = 'latitude'
    units = 'degrees_N'
    Data(grid_latitude(10), grid_longitude(9)) = [[53.941, ..., 50.225]] degrees_N

Auxiliary coordinate: longitude
    standard_name = 'longitude'
    units = 'degrees_E'
    Data(grid_longitude(9), grid_latitude(10)) = [[2.004, ..., 8.156]] degrees_E

Auxiliary coordinate: long_name=Grid latitude name
    long_name = 'Grid latitude name'
    Data(grid_latitude(10)) = [--, ..., 'kappa']

Domain ancillary: ncvar%a
    units = 'm'
    Data(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
    Bounds:Data(atmosphere_hybrid_height_coordinate(1), 2) = [[5.0, 15.0]]

Domain ancillary: ncvar%b
    Data(atmosphere_hybrid_height_coordinate(1)) = [20.0]
    Bounds:Data(atmosphere_hybrid_height_coordinate(1), 2) = [[14.0, 26.0]]

Domain ancillary: surface_altitude
    standard_name = 'surface_altitude'
    units = 'm'
    Data(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 270.0]] m

Coordinate reference: atmosphere_hybrid_height_coordinate
    Coordinate conversion:computed_standard_name = altitude
    Coordinate conversion:standard_name = atmosphere_hybrid_height_coordinate
    Coordinate conversion:a = Domain Ancillary: ncvar%a
    Coordinate conversion:b = Domain Ancillary: ncvar%b
    Coordinate conversion:orog = Domain Ancillary: surface_altitude
    Datum:earth_radius = 6371007
    Dimension Coordinate: atmosphere_hybrid_height_coordinate

Coordinate reference: rotated_latitude_longitude
    Coordinate conversion:grid_mapping_name = rotated_latitude_longitude
    Coordinate conversion:grid_north_pole_latitude = 38.0
    Coordinate conversion:grid_north_pole_longitude = 190.0
    Datum:earth_radius = 6371007
    Dimension Coordinate: grid_longitude
    Dimension Coordinate: grid_latitude
    Auxiliary Coordinate: longitude
    Auxiliary Coordinate: latitude

Cell measure: measure:area
    units = 'km2'
    Data(grid_longitude(9), grid_latitude(10)) = [[2391.9657, ..., 2392.6009]] km2

File inspection with cfa

The description for every field constructs found in datasets also be generated from the command line, with minimal, medium or full detail, by using the cfa tool, for example:

Use cfa on the command line to inspect the field constructs contained in one or more datasets. The “-1” option treats all input files collectively as a single CF dataset, so that aggregation is attempted within and between the input files.

$ cfa file.nc
CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
CF Field: specific_humidity(latitude(5), longitude(8)) 1
$ cfa -1 *.nc
CF Field: specific_humidity(cf_role=timeseries_id(4), ncdim%timeseries(9))
CF Field: cell_area(ncdim%longitude(9), ncdim%latitude(10)) m2
CF Field: eastward_wind(latitude(10), longitude(9)) m s-1
CF Field: specific_humidity(latitude(5), longitude(8)) 1
CF Field: air_potential_temperature(time(120), latitude(5), longitude(8)) K
CF Field: precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1
CF Field: precipitation_flux(time(2), latitude(4), longitude(5)) kg m2 s-1
CF Field: air_temperature(time(2), latitude(73), longitude(96)) K
CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K

cfa may also be used to write aggregated field constructs to new datasets, and may be used with external files.

---

Visualization

Powerful, flexible, and very simple to produce visualizations of field constructs are available with the cfplot package (that needs to be installed separately to cf, see http://ajheaps.github.io/cf-plot for details).

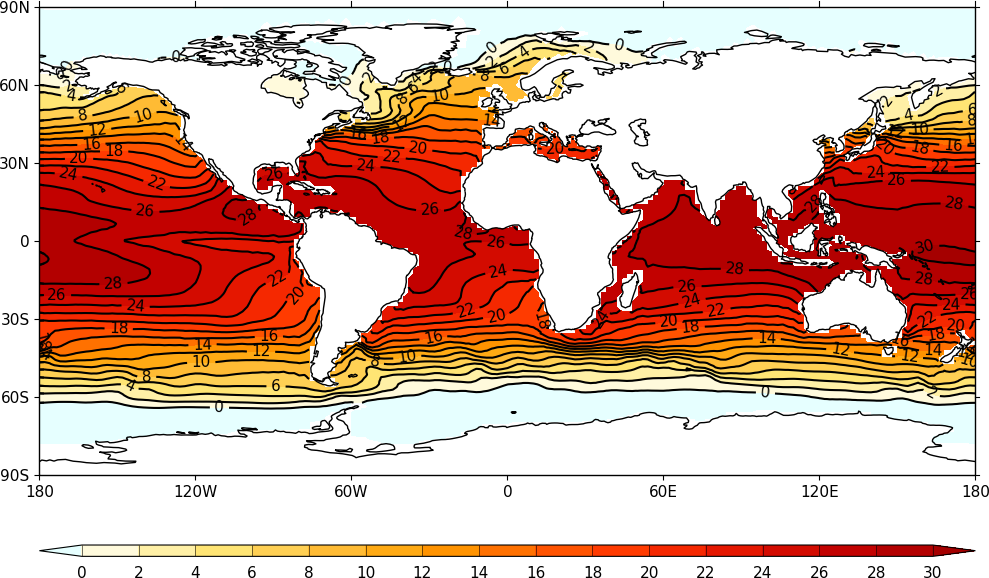
Example output of cfplot displaying a cf field construct.

See the cfplot gallery for the wide range of plotting possibilities, with example code. These include, but are not limited to:

• Cylindrical, polar stereographic and other plane projections

• Latitude or longitude vs. height or pressure

• Hovmuller

• Vectors

• Stipples

• Multiple plots on a page

• Colour scales

• User defined axes

• Rotated pole

• Irregular grids

• Trajectories

• Line plots

---

Field lists

A field list, contained in a cf.FieldList instance, is an ordered sequence of field constructs. It supports all of the Python list operations, such as indexing, iteration, and methods like append.

List-like operations on field list instances.

>>> x = cf.read('file.nc')
>>> y = cf.read('precipitation_flux.nc')
>>> x
[<CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>]
>>> y
[<CF Field: precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1>]
>>> y.extend(x)
>>> y
[<CF Field: precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1>,
 <CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>]
>>> y[2]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>
>>> y[::-1]
[<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>,
 <CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1>]
>>> len(y)
3
>>> len(y + y)
6
>>> len(y * 4)
12
>>> for f in y:
...     print('field:', repr(f))
...
field: <CF Field: precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1>
field: <CF Field: specific_humidity(latitude(5), longitude(8)) 1>
field: <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>

The field list also has some additional methods for copying, testing equality, sorting and selection.

---

Properties

Descriptive properties that apply to field construct as a whole may be retrieved with the properties method:

Retrieve all of the descriptive properties

>>> q, t = cf.read('file.nc')
>>> t.properties()
{'Conventions': 'CF-1.7',
 'project': 'research',
 'standard_name': 'air_temperature',
 'units': 'K'}

Note

From a Python script or using the standard Python shell, the result of methods such as the property methods given here will be returned in condensed form, without linebreaks between items.

If a “pretty printed” output as displayed in these pages is preferred, use the ipython shell or wrap calls with a suitable method from Python’s dedicated pprint module.

Individual properties may be accessed and modified with the del_property, get_property, has_property, and set_property methods:

Check is a property exists, retrieve its value, delete it and then set it to a new value.

>>> t.has_property('standard_name')
True
>>> t.get_property('standard_name')
'air_temperature'
>>> t.del_property('standard_name')
'air_temperature'
>>> t.get_property('standard_name', default='not set')
'not set'
>>> t.set_property('standard_name', value='air_temperature')
>>> t.get_property('standard_name', default='not set')
'air_temperature'

A collection of properties may be set at the same time with the set_properties method of the field construct, and all properties may be completely removed with the clear_properties method.

Update the properties with a collection, delete all of the properties, and reinstate the original properties.

>>> original = t.properties()
>>> original
{'Conventions': 'CF-1.7',
 'project': 'research',
 'standard_name': 'air_temperature',
 'units': 'K'}
>>> t.set_properties({'foo': 'bar', 'units': 'K'})
>>> t.properties()
{'Conventions': 'CF-1.7',
 'foo': 'bar',
 'project': 'research',
 'standard_name': 'air_temperature',
 'units': 'K'}
>>> t.clear_properties()
 {'Conventions': 'CF-1.7',
 'foo': 'bar',
 'project': 'research',
 'standard_name': 'air_temperature',
 'units': 'K'}
>>> t.properties()
{'units': 'K'}
>>> t.set_properties(original)
>>> t.properties()
{'Conventions': 'CF-1.7',
 'project': 'research',
 'standard_name': 'air_temperature',
 'units': 'K'}

Note that the “units” property persisted after the call to the clear_properties method because is it deeply associated with the field construct’s data, which still exists.

All of the methods related to the properties are listed here.

Field identities

A field construct identity is a string that describes the construct and is based on the field construct’s properties. A canonical identity is returned by the identity method of the field construct, and all possible identities are returned by the identities method.

A field construct’s identity may be any one of the following

• The value of the standard_name property, e.g. 'air_temperature',

• The value of the id attribute, preceded by 'id%=',

• The value of any property, preceded by the property name and an equals, e.g. 'long_name=Air Temperature', 'foo=bar', etc.,

• The netCDF variable name, preceded by “ncvar%”, e.g. 'ncvar%tas' (see the netCDF interface),

Get the canonical identity, and all identities, of a field construct.

>>> t.identity()
'air_temperature'
>>> t.identities()
['air_temperature',
 'Conventions=CF-1.7',
 'project=research',
 'units=K',
 'standard_name=air_temperature',
 'ncvar%ta']

The identity returned by the identity method is, by default, the least ambiguous identity (defined in the method documentation), but it may be restricted to the standard_name property and id attribute; or also the long_name property and netCDF variable name (see the netCDF interface). See the strict and relaxed keywords.

---

Metadata constructs

The metadata constructs describe the field construct that contains them. Each CF data model metadata construct has a corresponding cf class:

Class	CF data model construct	Description
cf.DomainAxis	Domain axis	Independent axes of the domain
cf.DimensionCoordinate	Dimension coordinate	Domain cell locations
cf.AuxiliaryCoordinate	Auxiliary coordinate	Domain cell locations
cf.CoordinateReference	Coordinate reference	Domain coordinate systems
cf.DomainAncillary	Domain ancillary	Cell locations in alternative coordinate systems
cf.CellMeasure	Cell measure	Domain cell size or shape
cf.FieldAncillary	Field ancillary	Ancillary metadata which vary within the domain
cf.CellMethod	Cell method	Describes how data represent variation within cells

Metadata constructs of a particular type can be retrieved with the following attributes of the field construct:

Attribute	Metadata constructs
domain_axes	Domain axes
dimension_coordinates	Dimension coordinates
auxiliary_coordinates	Auxiliary coordinates
coordinate_references	Coordinate references
domain_ancillaries	Domain ancillaries
cell_measures	Cell measures
field_ancillaries	Field ancillaries
cell_methods	Cell methods

Each of these attributes returns a cf.Constructs class instance that maps metadata constructs to unique identifiers called “construct keys”. A cf.Constructs instance has methods for selecting constructs that meet particular criteria (see Filtering metadata constructs). It also behaves like a “read-only” Python dictionary, in that it has items, keys and values methods that work exactly like their corresponding dict methods. It also has a get method and indexing like a Python dictionary (see Metadata construct access for details).

Retrieve the field construct’s coordinate reference constructs, and access them using dictionary methods.

>>> q, t = cf.read('file.nc')
>>> t.coordinate_references
<CF Constructs: coordinate_reference(2)>
>>> print(t.coordinate_references)
Constructs:
{'coordinatereference0': <CF CoordinateReference: standard_name:atmosphere_hybrid_height_coordinate>,
 'coordinatereference1': <CF CoordinateReference: grid_mapping_name:rotated_latitude_longitude>}
>>> list(t.coordinate_references.keys())
['coordinatereference0', 'coordinatereference1']
>>> for key, value in t.coordinate_references.items():
...     print(key, repr(value))
...
coordinatereference0 <CF CoordinateReference: standard_name:atmosphere_hybrid_height_coordinate>
coordinatereference1 <CF CoordinateReference: grid_mapping_name:rotated_latitude_longitude>

Retrieve the field construct’s dimension coordinate and domain axis constructs.

>>> print(t.dimension_coordinates)
Constructs:
{'dimensioncoordinate0': <CF DimensionCoordinate: atmosphere_hybrid_height_coordinate(1) >,
 'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>,
 'dimensioncoordinate2': <CF DimensionCoordinate: grid_longitude(9) degrees>,
 'dimensioncoordinate3': <CF DimensionCoordinate: time(1) days since 2018-12-01 >}
>>> print(t.domain_axes)
Constructs:
{'domainaxis0': <CF DomainAxis: size(1)>,
 'domainaxis1': <CF DomainAxis: size(10)>,
 'domainaxis2': <CF DomainAxis: size(9)>,
 'domainaxis3': <CF DomainAxis: size(1)>}

The construct keys (e.g. 'domainaxis1') are usually generated internally and are unique within the field construct. However, construct keys may be different for equivalent metadata constructs from different field constructs, and for different Python sessions.

Metadata constructs of all types may be returned by the constructs attribute of the field construct:

Retrieve all of the field construct’s metadata constructs.

>>> q.constructs
<CF Constructs: cell_method(1), dimension_coordinate(3), domain_axis(3)>
>>> print(q.constructs)
Constructs:
{'cellmethod0': <CF CellMethod: area: mean>,
 'dimensioncoordinate0': <CF DimensionCoordinate: latitude(5) degrees_north>,
 'dimensioncoordinate1': <CF DimensionCoordinate: longitude(8) degrees_east>,
 'dimensioncoordinate2': <CF DimensionCoordinate: time(1) days since 2018-12-01 >,
 'domainaxis0': <CF DomainAxis: size(5)>,
 'domainaxis1': <CF DomainAxis: size(8)>,
 'domainaxis2': <CF DomainAxis: size(1)>}
>>> t.constructs
<CF Constructs: auxiliary_coordinate(3), cell_measure(1), cell_method(2), coordinate_reference(2), dimension_coordinate(4), domain_ancillary(3), domain_axis(4), field_ancillary(1)>
>>> print(t.constructs)
Constructs:
{'auxiliarycoordinate0': <CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>,
 'auxiliarycoordinate1': <CF AuxiliaryCoordinate: longitude(9, 10) degrees_E>,
 'auxiliarycoordinate2': <CF AuxiliaryCoordinate: long_name=Grid latitude name(10) >,
 'cellmeasure0': <CF CellMeasure: measure:area(9, 10) km2>,
 'cellmethod0': <CF CellMethod: domainaxis1: domainaxis2: mean where land (interval: 0.1 degrees)>,
 'cellmethod1': <CF CellMethod: domainaxis3: maximum>,
 'coordinatereference0': <CF CoordinateReference: standard_name:atmosphere_hybrid_height_coordinate>,
 'coordinatereference1': <CF CoordinateReference: grid_mapping_name:rotated_latitude_longitude>,
 'dimensioncoordinate0': <CF DimensionCoordinate: atmosphere_hybrid_height_coordinate(1) >,
 'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>,
 'dimensioncoordinate2': <CF DimensionCoordinate: grid_longitude(9) degrees>,
 'dimensioncoordinate3': <CF DimensionCoordinate: time(1) days since 2018-12-01 >,
 'domainancillary0': <CF DomainAncillary: ncvar%a(1) m>,
 'domainancillary1': <CF DomainAncillary: ncvar%b(1) >,
 'domainancillary2': <CF DomainAncillary: surface_altitude(10, 9) m>,
 'domainaxis0': <CF DomainAxis: size(1)>,
 'domainaxis1': <CF DomainAxis: size(10)>,
 'domainaxis2': <CF DomainAxis: size(9)>,
 'domainaxis3': <CF DomainAxis: size(1)>,
 'fieldancillary0': <CF FieldAncillary: air_temperature standard_error(10, 9) K>}

---

Data

The field construct’s data is stored in a cf.Data class instance that is accessed with the data attribute of the field construct.

Retrieve the data and inspect it, showing the shape and some illustrative values.

>>> q, t = cf.read('file.nc')
>>> t.data
<CF Data(1, 10, 9): [[[262.8, ..., 269.7]]] K>

The cf.Data instance provides access to the full array of values, as well as attributes to describe the array and methods for describing any data compression. However, the field construct (and any other construct that contains data) also provides attributes for direct access.

Retrieve a numpy array of the data.

>>> print(t.array)
[[[262.8 270.5 279.8 269.5 260.9 265.0 263.5 278.9 269.2]
  [272.7 268.4 279.5 278.9 263.8 263.3 274.2 265.7 279.5]
  [269.7 279.1 273.4 274.2 279.6 270.2 280.  272.5 263.7]
  [261.7 260.6 270.8 260.3 265.6 279.4 276.9 267.6 260.6]
  [264.2 275.9 262.5 264.9 264.7 270.2 270.4 268.6 275.3]
  [263.9 263.8 272.1 263.7 272.2 264.2 260.  263.5 270.2]
  [273.8 273.1 268.5 272.3 264.3 278.7 270.6 273.0 270.6]
  [267.9 273.5 279.8 260.3 261.2 275.3 271.2 260.8 268.9]
  [270.9 278.7 273.2 261.7 271.6 265.8 273.  278.5 266.4]
  [276.4 264.2 276.3 266.1 276.1 268.1 277.  273.4 269.7]]]

Inspect the data type, number of dimensions, dimension sizes and number of elements of the data.

>>> t.dtype
dtype('float64')
>>> t.ndim
3
>>> t.shape
(1, 10, 9)
>>> t.size
90

The field construct also has a get_data method as an alternative means of retrieving the data instance, which allows for a default to be returned if no data have been set; as well as a del_data method for removing the data.

All of the methods and attributes related to the data are listed here.

Data axes

The data array of the field construct spans all the domain axis constructs with the possible exception of size one domain axis constructs. The domain axis constructs spanned by the field construct’s data are found with the get_data_axes method of the field construct. For example, the data of the field construct t does not span the size one domain axis construct with key 'domainaxis3'.

Show which data axis constructs are spanned by the field construct’s data.

>>> print(t.domain_axes)
Constructs:
{'domainaxis0': <CF DomainAxis: size(1)>,
 'domainaxis1': <CF DomainAxis: size(10)>,
 'domainaxis2': <CF DomainAxis: size(9)>,
 'domainaxis3': <CF DomainAxis: size(1)>}
>>> t
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>
>>> t.data.shape
(1, 10, 9)
>>> t.get_data_axes()
('domainaxis0', 'domainaxis1', 'domainaxis2')

The data may be set with the set_data method of the field construct. The domain axis constructs spanned by the data are inferred from the existing domain axis constructs, provided that there are no ambiguities (such as two dimensions of the same size), in which case they can be explicitly provided via their construct keys. In any case, the data axes may be set at any time with the set_data_axes method of the field construct.

Delete the data and then reinstate it, using the existing data axes.

>>> data = t.del_data()
>>> t.has_data()
False
>>> t.set_data(data)
>>> t.data
<CF Data(1, 10, 9): [[[262.8, ..., 269.7]]] K>

See the section field construct creation for more examples.

Date-time

Data representing date-times is defined as elapsed times since a reference date-time in a particular calendar (Gregorian, by default). The array attribute of the cf.Data instance (and any construct that contains it) returns the elapsed times, and the datetime_array (and any construct that contains it) returns the data as an array of date-time objects.

View date-times aas elapsed time or as date-time objects.

>>> d = cf.Data([1, 2, 3], units='days since 2004-2-28')
>>> print(d.array)
[1 2 3]
>>> print(d.datetime_array)
[cftime.DatetimeGregorian(2004-02-29 00:00:00)
 cftime.DatetimeGregorian(2004-03-01 00:00:00)
 cftime.DatetimeGregorian(2004-03-02 00:00:00)]
>>> e = cf.Data([1, 2, 3], units='days since 2004-2-28', calendar='360_day')
>>> print(e.array)
[1 2 3]
>>> print(e.datetime_array)
[cftime.Datetime360Day(2004-02-29 00:00:00)
 cftime.Datetime360Day(2004-02-30 00:00:00)
 cftime.Datetime360Day(2004-03-01 00:00:00)]

Alternatively, date-time data may be created by providing date-time objects or ISO 8601-like date-time strings. Date-time objects may be cftime.datetime instances (as returned by the cf.dt and cf.dt_vector functions), Python datetime.datetime instances, or any other date-time object that has an equivalent API.

Creating a Data instance from a date-time objects.

>>> date_time = cf.dt(2004, 2, 29)
>>> date_time
cftime.datetime(2004-02-29 00:00:00)
>>> d = cf.Data(date_time, calendar='gregorian')
>>> print(d.array)
0.0
>>> d.datetime_array
array(cftime.DatetimeGregorian(2004-02-29 00:00:00), dtype=object)

Creating Data instances from date-time an array of date-time objects.

>>> date_times  = cf.dt_vector(['2004-02-29', '2004-02-30', '2004-03-01'], calendar='360_day')
>>> print (date_times)
[cftime.Datetime360Day(2004-02-29 00:00:00)
 cftime.Datetime360Day(2004-02-30 00:00:00)
 cftime.Datetime360Day(2004-03-01 00:00:00)]
>>> e = cf.Data(date_times)
>>> print(e.array)
[0. 1. 2.]
>>> print(e.datetime_array)
[cftime.Datetime360Day(2004-02-29 00:00:00)
 cftime.Datetime360Day(2004-02-30 00:00:00)
 cftime.Datetime360Day(2004-03-01 00:00:00)]

Creating Data instances from date-time strings. If no units or calendar are provided then the “dt” keyword is required.

>>> d = cf.Data(['2004-02-29', '2004-02-30', '2004-03-01'], calendar='360_day')
>>> d.Units
<Units: days since 2004-02-29 360_day>
>>> print(d.array)
[0. 1. 2.]
>>> print(d.datetime_array)
[cftime.Datetime360Day(2004-02-29 00:00:00)
 cftime.Datetime360Day(2004-02-30 00:00:00)
 cftime.Datetime360Day(2004-03-01 00:00:00)]
>>> e = cf.Data(['2004-02-29', '2004-03-01', '2004-03-02'], dt=True)
>>> e.Units
<Units: days since 2004-02-29>
>>> print(e.datetime_array)
[cftime.DatetimeGregorian(2004-02-29 00:00:00)
 cftime.DatetimeGregorian(2004-03-01 00:00:00)
 cftime.DatetimeGregorian(2004-03-02 00:00:00)]
>>> f = cf.Data(['2004-02-29', '2004-03-01', '2004-03-02'])
>>> print(f.array)
['2004-02-29' '2004-03-01' '2004-03-02']
>>> f.Units
<Units: >
>>> print(f.datetime_array)  # Raises Exception
Traceback (most recent call last):
    ...
ValueError: Can't create date-time array from units <Units: >

Manipulating dimensions

The dimensions of a field construct’s data may be reordered, have size one dimensions removed and have new new size one dimensions included by using the following field construct methods:

Method	Description
flatten	Flatten domain axes of the field construct
flip	Reverse the direction of a data dimension
insert_dimension	Insert a new size one data dimension. The new dimension must correspond to an existing size one domain axis construct.
squeeze	Remove size one data dimensions
transpose	Reorder data dimensions
unsqueeze	Insert all missing size one data dimensions

Remove all size one dimensions from the data, noting that metadata constructs which span the corresponding domain axis construct are not affected.

>>> q, t = cf.read('file.nc')
>>> t
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>
>>> t2 = t.squeeze()
>>> t2
<CF Field: air_temperature(grid_latitude(10), grid_longitude(9)) K>
>>> print(t2.dimension_coordinates)
Constructs:
{'dimensioncoordinate0': <CF DimensionCoordinate: atmosphere_hybrid_height_coordinate(1) >,
 'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>,
 'dimensioncoordinate2': <CF DimensionCoordinate: grid_longitude(9) degrees>,
 'dimensioncoordinate3': <CF DimensionCoordinate: time(1) days since 2018-12-01 >}

Insert a new size one dimension, corresponding to a size one domain axis construct, and then reorder the dimensions.

>>> t3 = t2.insert_dimension(axis='domainaxis3', position=1)
>>> t3
<CF Field: air_temperature(grid_latitude(10), time(1), grid_longitude(9)) K>
>>> t3.transpose([2, 0, 1])
<CF Field: air_temperature(grid_longitude(9), grid_latitude(10), time(1)) K>

When transposing the data dimensions, the dimensions of metadata construct data are, by default, unchanged. It is also possible to permute the data dimensions of the metadata constructs so that they have the same relative order as the field construct:

Also permute the data dimension of metadata constructs using the ‘contructs’ keyword.

>>> t4 = t.transpose(['X', 'Z', 'Y'], constructs=True)

Data mask

There is always a data mask, which may be thought of as a separate data array of booleans with the same shape as the original data. The data mask is False where the the data has values, and True where the data is missing. The data mask may be inspected with the mask attribute of the field construct, which returns the data mask in a field construct with the same metadata constructs as the original field construct.

Inspect the data mask of a field constuct.

>>> print(q)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(q.mask)
Field: long_name=mask
---------------------
Data            : long_name=mask(latitude(5), longitude(8))
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(q.mask.array)
[[False False False False False False False False]
 [False False False False False False False False]
 [False False False False False False False False]
 [False False False False False False False False]
 [False False False False False False False False]]

Mask the polar rows (see the “Assignment by index” section) and inspect the new data mask.

>>> q[[0, 4], :] = cf.masked
>>> print(q.mask.array)
[[ True  True  True  True  True  True  True  True]
 [False False False False False False False False]
 [False False False False False False False False]
 [False False False False False False False False]
 [ True  True  True  True  True  True  True  True]]

The _FillValue and missing_value attributes of the field construct are not stored as values of the field construct’s data. They are only used when writing the data to a netCDF dataset. Therefore testing for missing data by testing for equality to one of these property values will produce incorrect results; the any and all methods of the field construct should be used instead.

See if all, or any, data points are masked.

>>> q.mask.all()
False
>>> q.mask.any()
True

---

Subspacing by index

Creation of a new field construct which spans a subspace of the domain of an existing field construct is achieved either by indexing the field construct directly (as described in this section) or by identifying indices based on the metadata constructs (see Subspacing by metadata). The subspacing operation, in either case, also subspaces any metadata constructs of the field construct (e.g. coordinate metadata constructs) which span any of the domain axis constructs that are affected. The new field construct is created with the same properties as the original field construct.

Subspacing by indexing uses rules that are very similar to the numpy indexing rules, the only differences being:

• An integer index i specified for a dimension reduces the size of this dimension to unity, taking just the i-th element, but keeps the dimension itself, so that the rank of the array is not reduced.

• When two or more dimensions’ indices are sequences of integers then these indices work independently along each dimension (similar to the way vector subscripts work in Fortran). This is the same indexing behaviour as on a Variable object of the netCDF4 package.

• For a dimension that is cyclic, a range of indices specified by a slice that spans the edges of the data (such as -2:3 or 3:-2:-1) is assumed to “wrap” around, rather then producing a null result.

Create a new field construct whose domain spans the first longitude of the original, and with a reversed latitude axis.

>>> q, t = cf.read('file.nc')
>>> print(q)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: time(1) = [2019-01-01 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east

>>> new = q[::-1, 0]
>>> print(new)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(1)) 1
Cell methods    : area: mean
Dimension coords: time(1) = [2019-01-01 00:00:00]
                : latitude(5) = [75.0, ..., -75.0] degrees_north
                : longitude(1) = [22.5] degrees_east

Create new field constructs with a variety of indexing techniques.

>>> t
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>
>>> t[:, :, 1]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(1)) K>
>>> t[:, 0]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(1), grid_longitude(9)) K>
>>> t[..., 6:3:-1, 3:6]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(3), grid_longitude(3)) K>
>>> t[0, [2, 3, 9], [4, 8]]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(3), grid_longitude(2)) K>
>>> t[0, :, -2]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(1)) K>
>>> t[..., [True, False, True, True, False, False, True, False, False]]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(4)) K>

Subspacing a cyclic dimension with a slice will wrap around the data edges.

>>> q
<CF Field: specific_humidity(latitude(5), longitude(8)) 1>
>>> q.cyclic()
{'domainaxis1'}
>>> q.constructs.domain_axis_identity('domainaxis1')
'longitude'
>>> print(q[:, -2:3])
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(5)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(5) = [-67.5, ..., 112.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(q[:, 3:-2:-1])
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(5)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(5) = [157.5, ..., -22.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]

A cf.Data instance can also directly be indexed in the same way:

Create a new ‘Data’ instance by indexing.

>>> t.data[0, [2, 3, 9], [4, 8]]
<CF Data(1, 3, 2): [[[279.6, ..., 269.7]]] K>

---

Assignment by index

Data elements can be changed by assigning to elements selected by indices of the data (as described in this section); by conditions based on the data values of the field construct or one of its metadata constructs (see Assignment by condition); or by identifying indices based on arbitrary metadata constructs (see Assignment by metadata).

Assignment by indices uses rules that are very similar to the numpy indexing rules, the only difference being:

• When two or more dimensions’ indices are sequences of integers then these indices work independently along each dimension (similar to the way vector subscripts work in Fortran). This is the same indexing behaviour as on a Variable object of the netCDF4 package.

• For a dimension that is cyclic, a range of indices specified by a slice that spans the edges of the data (such as -2:3 or 3:-2:-1) is assumed to “wrap” around, rather then producing a null result.

A single value may be assigned to any number of elements.

Set a single element to -1, a “column” of elements to -2 and a “square” of elements to -3.

>>> q, t = cf.read('file.nc')
>>> t[:, 0, 0] = -1
>>> t[:, :, 1] = -2
>>> t[..., 6:3:-1, 3:6] = -3
>>> print(t.array)
[[[ -1.0  -2.0 279.8 269.5 260.9 265.0 263.5 278.9 269.2]
  [272.7  -2.0 279.5 278.9 263.8 263.3 274.2 265.7 279.5]
  [269.7  -2.0 273.4 274.2 279.6 270.2 280.0 272.5 263.7]
  [261.7  -2.0 270.8 260.3 265.6 279.4 276.9 267.6 260.6]
  [264.2  -2.0 262.5  -3.0  -3.0  -3.0 270.4 268.6 275.3]
  [263.9  -2.0 272.1  -3.0  -3.0  -3.0 260.0 263.5 270.2]
  [273.8  -2.0 268.5  -3.0  -3.0  -3.0 270.6 273.0 270.6]
  [267.9  -2.0 279.8 260.3 261.2 275.3 271.2 260.8 268.9]
  [270.9  -2.0 273.2 261.7 271.6 265.8 273.0 278.5 266.4]
  [276.4  -2.0 276.3 266.1 276.1 268.1 277.0 273.4 269.7]]]

An array of values can be assigned, as long as it is broadcastable to the shape defined by the indices, using the numpy broadcasting rules.

Assigning arrays of values.

>>> import numpy
>>> t[..., 6:3:-1, 3:6] = numpy.arange(9).reshape(3, 3)
>>> t[0, [2, 9], [4, 8]] =  cf.Data([[-4, -5]])
>>> t[0, [4, 7], 0] = [[-10], [-11]]
>>> print(t.array)
[[[ -1.0  -2.0 279.8 269.5 260.9 265.0 263.5 278.9 269.2]
  [272.7  -2.0 279.5 278.9 263.8 263.3 274.2 265.7 279.5]
  [269.7  -2.0 273.4 274.2  -4.0 270.2 280.0 272.5  -5.0]
  [261.7  -2.0 270.8 260.3 265.6 279.4 276.9 267.6 260.6]
  [-10.0  -2.0 262.5   6.0   7.0   8.0 270.4 268.6 275.3]
  [263.9  -2.0 272.1   3.0   4.0   5.0 260.0 263.5 270.2]
  [273.8  -2.0 268.5   0.0   1.0   2.0 270.6 273.0 270.6]
  [-11.0  -2.0 279.8 260.3 261.2 275.3 271.2 260.8 268.9]
  [270.9  -2.0 273.2 261.7 271.6 265.8 273.0 278.5 266.4]
  [276.4  -2.0 276.3 266.1  -4.0 268.1 277.0 273.4  -5.0]]]

In-place modification is also possible:

Modifying the data in-place.

>>> print(t[0, 0, -1].array)
[[[269.2]]]
>>> t[0, 0, -1] /= -10
>>> print(t[0, 0, -1].array)
[[[-26.92]]]

A cf.Data instance can also assigned values in the same way:

Assign to the ‘Data’ instance directly.

>>> t.data[0, 0, -1] = -99
>>> print(t[0, 0, -1].array)
[[[-99.]]]

Masked values

Data array elements may be set to masked values by assigning them to the cf.masked constant, thereby updating the the data mask.

Set a column of elements to masked values.

>>> t[0, :, -2] = cf.masked
>>> print(t.array)
[[[ -1.0  -2.0 279.8 269.5 260.9 265.0 263.5    -- -99.0]
  [272.7  -2.0 279.5 278.9 263.8 263.3 274.2    -- 279.5]
  [269.7  -2.0 273.4 274.2  -4.0 270.2 280.0    --  -5.0]
  [261.7  -2.0 270.8 260.3 265.6 279.4 276.9    -- 260.6]
  [264.2  -2.0 262.5   6.0   7.0   8.0 270.4    -- 275.3]
  [263.9  -2.0 272.1   3.0   4.0   5.0 260.0    -- 270.2]
  [273.8  -2.0 268.5   0.0   1.0   2.0 270.6    -- 270.6]
  [-11.0  -2.0 279.8 260.3 261.2 275.3 271.2    -- 268.9]
  [270.9  -2.0 273.2 261.7 271.6 265.8 273.0    -- 266.4]
  [276.4  -2.0 276.3 266.1  -4.0 268.1 277.0    --  -5.0]]]

By default the data mask is “hard”, meaning that masked values can not be changed by assigning them to another value. This behaviour may be changed by setting the hardmask attribute of the field construct to False, thereby making the data mask “soft”.

Changing masked elements back to data values is only possible when the “hardmask” attribute is False.

>>> t[0, 4, -2] = 99
>>> print(t[0, 4, -2].array)
[[[--]]]
>>> t.hardmask = False
>>> t[0, 4, -2] = 99
>>> print(t[0, 4, -2].array)
[[[99.]]]

Note that this is the opposite behaviour to numpy arrays, which assume that the mask is soft by default. The reason for the difference is so that land-sea masks are, by default, preserved through assignment operations.

Assignment from other field constructs

Another field construct can also be assigned to indices. The other field construct’s data is actually assigned, but only after being transformed so that it is broadcastable to the subspace defined by the assignment indices. This is done by using the metadata constructs of the two field constructs to create a mapping of physically compatible dimensions between the fields, and then manipulating the dimensions of the other field construct’s data to ensure that they are broadcastable.

Transform a field construct’s data and assign it back to the original field, demonstrating that this is a null operation.

>>> q, t = cf.read('file.nc')
>>> t0 = t.copy()
>>> u = t.squeeze(0)
>>> u.transpose(inplace=True)
>>> u.flip(inplace=True)
>>> t[...] = u
>>> t.allclose(t0)
True

Broadcasting is carried out after transforms to ensure field construct compatibility.

>>> print(t[:, :, 1:3].array)
[[[270.5 279.8]
   [268.4 279.5]
   [279.1 273.4]
   [260.6 270.8]
   [275.9 262.5]
   [263.8 272.1]
   [273.1 268.5]
   [273.5 279.8]
   [278.7 273.2]
   [264.2 276.3]]]
>>> print(u[2].array)
[[277.  273.  271.2 270.6 260.  270.4 276.9 280.  274.2 263.5]]
>>> t[:, :, 1:3] = u[2]
>>> print(t[:, :, 1:3].array)
[[[263.5 263.5]
  [274.2 274.2]
  [280.  280. ]
  [276.9 276.9]
  [270.4 270.4]
  [260.  260. ]
  [270.6 270.6]
  [271.2 271.2]
  [273.  273. ]
  [277.  277. ]]]

If either of the field constructs does not have sufficient metadata to create the such a mapping, then any manipulation of the dimensions must be done manually, and the other field construct’s cf.Data instance (rather than the field construct itself) may be assigned.

---

Units

The field construct, and any metadata construct that contains data, has units which are described by the Units attribute that stores a cf.Units object (which is identical to a cfunits.Units object of the cfunits package). The units property provides the units contained in the cf.Units instance, and changes in one are reflected in the other.

Inspection and changing of units.

>>> q, t = cf.read('file.nc')
>>> t.units
'K'
>>> t.Units
<Units: K>
>>> t.units = 'degreesC'
>>> t.units
'degreesC'
>>> t.Units
<Units: degreesC>
>>> t.Units += 273.15
>>> t.units
'K'
>>> t.Units
<Units: K>

When the units are changed, the data are automatically converted to the new units when next accessed.

Changing the units automatically results converts the data values.

>>> t.data
<CF Data(1, 10, 9): [[[262.8, ..., 269.7]]] K>
>>> t.Units = cf.Units('degreesC')
>>> t.data
<CF Data(1, 10, 9): [[[-10.35, ..., -3.45]]] degreesC>
>>> t.units = 'Kelvin'
>>> t.data
<CF Data(1, 10, 9): [[[262.8, ..., 269.7]]] Kelvin>

When assigning to the data with values that have units, the values are automatically converted to have the same units as the data.

Automatic conversions occur when assigning from data with different units.

>>> t.data
<CF Data(1, 10, 9): [[[262.8, ..., 269.7]]] Kelvin>
>>> t[0, 0, 0] = cf.Data(1)
>>> t.data
<CF Data(1, 10, 9): [[[1.0, ..., 269.7]]] Kelvin>
>>> t[0, 0, 0] = cf.Data(1, 'degreesC')
>>> t.data
<CF Data(1, 10, 9): [[[274.15, ..., 269.7]]] Kelvin>

Automatic units conversions are also carried out between operands during mathematical operations.

Calendar

When the data represents date-times, the cf.Units instance describes both the units and calendar of the data. If the latter is missing then the Gregorian calender is assumed, as per the CF conventions. The calendar property provides the calendar contained in the cf.Units instance, and changes in one are reflected in the other.

The calendar of date-times is available as a property or via the Units instance.

>>> air_temp = cf.read('air_temperature.nc')[0]
>>> time = air_temp.coordinate('time')
>>> time.units
'days since 1860-1-1'
>>> time.calendar
'360_day'
>>> time.Units
<Units: days since 1860-1-1 360_day>

---

Filtering metadata constructs

A cf.Constructs instance has filtering methods for selecting constructs that meet various criteria:

Method	Filter criteria
filter_by_identity	Metadata construct identity
filter_by_type	Metadata construct type
filter_by_property	Property values
filter_by_axis	The domain axis constructs spanned by the data
filter_by_naxes	The number of domain axis constructs spanned by the data
filter_by_size	The size domain axis constructs
filter_by_measure	Measure value (for cell measure constructs)
filter_by_method	Method value (for cell method constructs)
filter_by_data	Whether or not there could be be data.
filter_by_key	Construct key
filter_by_ncvar	NetCDF variable name (see the netCDF interface)
filter_by_ncdim	NetCDF dimension name (see the netCDF interface)

Each of these methods returns a new cf.Constructs instance that contains the selected metadata constructs.

Get constructs by their type.

>>> q, t = cf.read('file.nc')
>>> print(t.constructs.filter_by_type('dimension_coordinate'))
Constructs:
{'dimensioncoordinate0': <CF DimensionCoordinate: atmosphere_hybrid_height_coordinate(1) >,
 'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>,
 'dimensioncoordinate2': <CF DimensionCoordinate: grid_longitude(9) degrees>,
 'dimensioncoordinate3': <CF DimensionCoordinate: time(1) days since 2018-12-01 >}
>>> print(t.constructs.filter_by_type('cell_method', 'field_ancillary'))
Constructs:
{'cellmethod0': <CF CellMethod: domainaxis1: domainaxis2: mean where land (interval: 0.1 degrees)>,
 'cellmethod1': <CF CellMethod: domainaxis3: maximum>,
 'fieldancillary0': <CF FieldAncillary: air_temperature standard_error(10, 9) K>}

Get constructs by their properties.

>>> print(t.constructs.filter_by_property(
...             standard_name='air_temperature standard_error'))
Constructs:
{'fieldancillary0': <CF FieldAncillary: air_temperature standard_error(10, 9) K>}
>>> print(t.constructs.filter_by_property(
...             standard_name='air_temperature standard_error',
...             units='K'))
Constructs:
{'fieldancillary0': <CF FieldAncillary: air_temperature standard_error(10, 9) K>}
>>> print(t.constructs.filter_by_property(
...             'or',
...             standard_name='air_temperature standard_error',
...             units='m'))
Constructs:
{'domainancillary0': <CF DomainAncillary: ncvar%a(1) m>,
 'domainancillary2': <CF DomainAncillary: surface_altitude(10, 9) m>,
 'fieldancillary0': <CF FieldAncillary: air_temperature standard_error(10, 9) K>}

Get constructs whose data span the ‘domainaxis1’ domain axis construct; and those which also do not span the ‘domainaxis2’ domain axis construct.

>>> print(t.constructs.filter_by_axis('and', 'domainaxis1'))
Constructs:
{'auxiliarycoordinate0': <CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>,
 'auxiliarycoordinate1': <CF AuxiliaryCoordinate: longitude(9, 10) degrees_E>,
 'auxiliarycoordinate2': <CF AuxiliaryCoordinate: long_name=Grid latitude name(10) >,
 'cellmeasure0': <CF CellMeasure: measure:area(9, 10) km2>,
 'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>,
 'domainancillary2': <CF DomainAncillary: surface_altitude(10, 9) m>,
 'fieldancillary0': <CF FieldAncillary: air_temperature standard_error(10, 9) K>}

Get cell measure constructs by their “measure”.

>>> print(t.constructs.filter_by_measure('area'))
Constructs:
{'cellmeasure0': <CF CellMeasure: measure:area(9, 10) km2>}

Get cell method constructs by their “method”.

>>> print(t.constructs.filter_by_method('maximum'))
Constructs:
{'cellmethod1': <CF CellMethod: domainaxis3: maximum>}

As each of these methods returns a cf.Constructs instance, it is easy to perform further filters on their results:

Make selections from previous selections.

>>> print(t.constructs.filter_by_type('auxiliary_coordinate').filter_by_axis('and', 'domainaxis2'))
Constructs:
{'auxiliarycoordinate0': <CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>,
 'auxiliarycoordinate1': <CF AuxiliaryCoordinate: longitude(9, 10) degrees_E>}
>>> c = t.constructs.filter_by_type('dimension_coordinate')
>>> d = c.filter_by_property(units='degrees')
>>> print(d)
Constructs:
{'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>,
 'dimensioncoordinate2': <CF DimensionCoordinate: grid_longitude(9) degrees>}

Construct identities

Another method of selection is by metadata construct “identity”. Construct identities are used to describe constructs when they are inspected, and so it is often convenient to copy these identities when selecting metadata constructs. For example, the three auxiliary coordinate constructs in the field construct t have identities 'latitude', 'longitude' and 'long_name=Grid latitude name'.

A construct’s identity may be any one of the following

• The value of the standard_name property, e.g. 'air_temperature',

• The value of the id attribute, preceded by 'id%=',

• The physical nature of the construct denoted by 'X', 'Y', 'Z' or 'T', denoting longitude (or x-projection), latitude (or y-projection), vertical and temporal constructs respectively,

• The value of any property, preceded by the property name and an equals, e.g. 'long_name=Air Temperature', 'axis=X', 'foo=bar', etc.,

• The cell measure, preceded by “measure:”, e.g. 'measure:volume'

• The cell method, preceded by “method:”, e.g. 'method:maximum'

• The netCDF variable name, preceded by “ncvar%”, e.g. 'ncvar%tas' (see the netCDF interface),

• The netCDF dimension name, preceded by “ncdim%” e.g. 'ncdim%z' (see the netCDF interface), and

• The construct key, optionally proceeded by “key%”, e.g. 'auxiliarycoordinate2' or 'key%auxiliarycoordinate2'.

Get constructs by their identity.

>>> print(t)
Field: air_temperature (ncvar%ta)
---------------------------------
Data            : air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
Cell methods    : grid_latitude(10): grid_longitude(9): mean where land (interval: 0.1 degrees) time(1): maximum
Field ancils    : air_temperature standard_error(grid_latitude(10), grid_longitude(9)) = [[0.81, ..., 0.78]] K
Dimension coords: time(1) = [2019-01-01 00:00:00]
                : atmosphere_hybrid_height_coordinate(1) = [1.5]
                : grid_latitude(10) = [2.2, ..., -1.76] degrees
                : grid_longitude(9) = [-4.7, ..., -1.18] degrees
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[53.941, ..., 50.225]] degrees_N
                : longitude(grid_longitude(9), grid_latitude(10)) = [[2.004, ..., 8.156]] degrees_E
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., 'kappa']
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[2391.9657, ..., 2392.6009]] km2
Coord references: grid_mappng_name:rotated_latitude_longitude
                : standard_name:atmosphere_hybrid_height_coordinate
Domain ancils   : ncvar%a(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
                : ncvar%b(atmosphere_hybrid_height_coordinate(1)) = [20.0]
                : surface_altitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 270.0]] m
>>> print(t.constructs.filter_by_identity('X'))
Constructs:
{'auxiliarycoordinate1': <CF AuxiliaryCoordinate: longitude(9, 10) degrees_E>,
 'dimensioncoordinate2': <CF DimensionCoordinate: grid_longitude(9) degrees>}
>>> print(t.constructs.filter_by_identity('latitude'))
Constructs:
{'auxiliarycoordinate0': <CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>}
>>> print(t.constructs.filter_by_identity('long_name=Grid latitude name'))
Constructs:
{'auxiliarycoordinate2': <CF AuxiliaryCoordinate: long_name=Grid latitude name(10) >}
>>> print(t.constructs.filter_by_identity('measure:area'))
Constructs:
{'cellmeasure0': <CF CellMeasure: measure:area(9, 10) km2>}
>>> print(t.constructs.filter_by_identity('ncvar%b'))
Constructs:
{'domainancillary1': <CF DomainAncillary: ncvar%b(1) >}

The identity returned by the identity method is, by default, the least ambiguous identity (defined in the method documentation), but it may be restricted in various ways. See the strict and relaxed keywords.

As a further convenience, selection by construct identity is also possible by providing identities to a call of a cf.Constructs instance itself, and this technique for selecting constructs by identity will be used in the rest of this tutorial:

Construct selection by identity is possible with via the “filter_by_identity” method, or directly from the “Constructs” instance.

>>> print(t.constructs.filter_by_identity('latitude'))
Constructs:
{'auxiliarycoordinate0': <CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>}
>>> print(t.constructs('latitude'))
Constructs:
{'auxiliarycoordinate0': <CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>}

Selection by construct key is useful for systematic metadata construct access, or for when a metadata construct is not identifiable by other means:

Get constructs by construct key.

>>> print(t.constructs.filter_by_key('domainancillary2'))
Constructs:
{'domainancillary2': <CF DomainAncillary: surface_altitude(10, 9) m>}
>>> print(t.constructs.filter_by_key('cellmethod1'))
Constructs:
{'cellmethod1': <CF CellMethod: domainaxis3: maximum>}
>>> print(t.constructs.filter_by_key('auxiliarycoordinate2', 'cellmeasure0'))
Constructs:
{'auxiliarycoordinate2': <CF AuxiliaryCoordinate: long_name=Grid latitude name(10) >,
 'cellmeasure0': <CF CellMeasure: measure:area(9, 10) km2>}

If no constructs match the given criteria, then an “empty” cf.Constructs instance is returned:

If no constructs meet the criteria then an empty “Constructs” object is returned.

>>> c = t.constructs('radiation_wavelength')
>>> c
<CF Constructs: >
>>> print(c)
Constructs:
{}
>>> len(c)
0

The constructs that were not selected by a filter may be returned by the inverse_filter method applied to the results of filters:

Get the constructs that were not selected by a filter.

>>> c = t.constructs.filter_by_type('auxiliary_coordinate')
>>> c
<CF Constructs: auxiliary_coordinate(3)>
>>> c.inverse_filter()
<CF Constructs: cell_measure(1), cell_method(2), coordinate_reference(2), dimension_coordinate(4), domain_ancillary(3), domain_axis(4), field_ancillary(1)>

Note that selection by construct type is equivalent to using the particular method of the field construct for retrieving that type of metadata construct:

The bespoke methods for retrieving constructs by type are equivalent to a selection on all of the metadata constructs.

>>> print(t.constructs.filter_by_type('cell_measure'))
Constructs:
{'cellmeasure0': <CF CellMeasure: measure:area(9, 10) km2>}
>>> print(t.cell_measures)
Constructs:
{'cellmeasure0': <CF CellMeasure: measure:area(9, 10) km2>}

---

Metadata construct access

An individual metadata construct, or its construct key, may be returned by any of the following techniques:

• with the construct method of a field construct,

Get the “latitude” metadata construct via its construct identity, and also its key.

>>> t.construct('latitude')
<CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>
>>> t.construct('latitude', key=True)
'auxiliarycoordinate0'

• with the construct_key and get_construct methods of a field construct:

Get the “latitude” metadata construct key with its construct identity and use the key to get the construct itself

>>> key = t.construct_key('latitude')
>>> t.get_construct(key)
<CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>

• with the value method of a cf.Constructs instance that contains one construct,

Get the “latitude” metadata construct via its identity and the ‘value’ method.

>>> t.constructs('latitude').value()
<CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>

• with the get method of a cf.Constructs instance, or

Get the “latitude” metadata construct via its construct key and the ‘get’ method.

>>> t.constructs.get(key)
<CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>

• by indexing a cf.Constructs instance with a construct key.

Get the “latitude” metadata construct via its construct key and indexing

>>> t.constructs[key]
<CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>

In addition, an individual metadata construct of a particular type can be retrieved with the following methods of the field construct:

Method	Metadata construct
domain_axis	Domain axis
dimension_coordinate	Dimension coordinate
auxiliary_coordinate	Auxiliary coordinate
coordinate_reference	Coordinate reference
domain_ancillary	Domain ancillary
cell_measure	Cell measure
field_ancillary	Field ancillary
cell_method	Cell method

These methods will only look for the given identity amongst constructs of the chosen type.

Get the “latitude” auxiliary coordinate construct via its construct identity, and also its key.

>>> t.auxiliary_coordinate('latitude')
<CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>
>>> t.auxiliary_coordinate('latitude', key=True)
'auxiliarycoordinate0'

The construct method of the field construct, the above methods for finding a construct of a particular type, and the value method of the cf.Constructs instance will all raise an exception of there is not a unique metadata construct to return, but this may be replaced with returning a default value or raising a customised exception:

By default an exception is raised if there is not a unique construct that meets the criteria. Alternatively, the value of the “default” parameter is returned.

>>> t.construct('measure:volume')  # Raises Exception
Traceback (most recent call last):
    ...
ValueError: Can't return zero constructs
>>> t.construct('measure:volume', False)
False
>>> c = t.constructs.filter_by_measure('volume')
>>> len(c)
0
>>> c.value()  # Raises Exception
Traceback (most recent call last):
    ...
ValueError: Can't return zero constructs
>>> c.value(default='No construct')
'No construct'
>>> c.value(default=KeyError('My message'))  # Raises Exception
Traceback (most recent call last):
    ...
KeyError: 'My message'
>>> d = t.constructs('units=degrees')
>>> len(d)
2
>>> d.value()  # Raises Exception
Traceback (most recent call last):
    ...
ValueError: Can't return 2 constructs
>>> print(d.value(default=None))
None

The get method of a cf.Constructs instance accepts an optional second argument to be returned if the construct key does not exist, exactly like the Python dict.get method.

Metadata construct properties

Metadata constructs share the same API as the field construct for accessing their properties:

Retrieve the “longitude” metadata construct, set a new property, and then inspect all of the properties.

>>> lon = q.construct('longitude')
>>> lon
<CF DimensionCoordinate: longitude(8) degrees_east>
>>> lon.set_property('long_name', 'Longitude')
>>> lon.properties()
{'units': 'degrees_east',
 'long_name': 'Longitude',
 'standard_name': 'longitude'}

Get the metadata construct with units of “km2”, find its canonical identity, and all of its valid identities, that may be used for selection by the “filter_by_identity” method

>>> area = t.constructs.filter_by_property(units='km2').value()
>>> area
<CF CellMeasure: measure:area(9, 10) km2>
>>> area.identity()
'measure:area'
>>> area.identities()
['measure:area', 'units=km2', 'ncvar%cell_measure']

Metadata construct data

Metadata constructs share the a similar API as the field construct as the field construct for accessing their data:

Retrieve the “longitude” metadata construct, inspect its data, change the third element of the array, and get the data as a numpy array.

>>> lon = q.constructs('longitude').value()
>>> lon
<CF DimensionCoordinate: longitude(8) degrees_east>
>>> lon.data
<CF Data(8): [22.5, ..., 337.5] degrees_east>
>>> lon.data[2]
<CF Data(1): [112.5] degrees_east>
>>> lon.data[2] = 133.33
>>> print(lon.array)
[ 22.5   67.5  133.33 157.5  202.5  247.5  292.5  337.5 ]
>>> lon.data[2] = 112.5

The domain axis constructs spanned by a particular metadata construct’s data are found with the get_data_axes method of the field construct:

Find the construct keys of the domain axis constructs spanned by the data of each metadata construct.

>>> key = t.construct_key('latitude')
>>> key
'auxiliarycoordinate0'
>>> t.get_data_axes(key)
('domainaxis1', 'domainaxis2')

The domain axis constructs spanned by all the data of all metadata construct may be found with the data_axes method of the field construct’s cf.Constructs instance:

Find the construct keys of the domain axis constructs spanned by the data of each metadata construct.

>>> t.constructs.data_axes()
{'auxiliarycoordinate0': ('domainaxis1', 'domainaxis2'),
 'auxiliarycoordinate1': ('domainaxis2', 'domainaxis1'),
 'auxiliarycoordinate2': ('domainaxis1',),
 'cellmeasure0': ('domainaxis2', 'domainaxis1'),
 'dimensioncoordinate0': ('domainaxis0',),
 'dimensioncoordinate1': ('domainaxis1',),
 'dimensioncoordinate2': ('domainaxis2',),
 'dimensioncoordinate3': ('domainaxis3',),
 'domainancillary0': ('domainaxis0',),
 'domainancillary1': ('domainaxis0',),
 'domainancillary2': ('domainaxis1', 'domainaxis2'),
 'fieldancillary0': ('domainaxis1', 'domainaxis2')}

A size one domain axis construct that is not spanned by the field construct’s data may still be spanned by the data of metadata constructs. For example, the data of the field construct t does not span the size one domain axis construct with key 'domainaxis3', but this domain axis construct is spanned by a “time” dimension coordinate construct (with key 'dimensioncoordinate3'). Such a dimension coordinate (i.e. one that applies to a domain axis construct that is not spanned by the field construct’s data) corresponds to a CF-netCDF scalar coordinate variable.

---

Time

Constructs (including the field constructs) that represent elapsed time have data array values that provide elapsed time since a reference date. These constructs are identified by the presence of “reference time” units. The data values may be converted into the date-time objects of the cftime package with the datetime_array attribute of the construct, or its cf.Data instance.

Inspect the the values of a “time” construct as elapsed times and as date-times.

>>> time = q.construct('time')
>>> time
<CF DimensionCoordinate: time(1) days since 2018-12-01 >
>>> time.get_property('units')
'days since 2018-12-01'
>>> time.get_property('calendar', default='standard')
'standard'
>>> print(time.array)
[31.]
>>> print(time.datetime_array)
[cftime.DatetimeGregorian(2019-01-01 00:00:00)]

Time duration

A period of time may stored in a cf.TimeDuration object. For many applications, a cf.Data instance with appropriate units (such as seconds) is equivalent, but a cf.TimeDuration instance also allows units of calendar years or months; and may be relative to a date-time offset.

Define a duration of one calendar month which, if applicable, starts at 12:00 on the 16th of the month.

>>> cm = cf.TimeDuration(1, 'calendar_month', day=16, hour=12)
>>> cm
<CF TimeDuration: P1M (Y-M-16 12:00:00)>

cf.TimeDuration objects support comparison and arithmetic operations with numeric scalars, cf.Data instances and date-time objects:

Add a calendar month to a date-time object, and a date-time data.

>>> cf.dt(2000, 2, 1) + cm
cftime.datetime(2000-03-01 00:00:00)
>>> cf.Data([1, 2, 3], 'days since 2000-02-01') + cm
<CF Data(3): [2000-03-02 00:00:00, 2000-03-03 00:00:00, 2000-03-04 00:00:00] gregorian>

Date-time ranges that span the time duration can also be created:

Create an interval starting from date-time; and an interval that contains a date-time, taking into account the offset.

>>> cm.interval(cf.dt(2000, 2, 1))
(cftime.DatetimeGregorian(2000-02-01 00:00:000),
 cftime.DatetimeGregorian(2000-03-01 00:00:000))
>>> cm.bounds(cf.dt(2000, 2, 1))
(cftime.DatetimeGregorian(2000-01-16 12:00:00),
 cftime.DatetimeGregorian(2000-02-16 12:00:00))

Time duration constructors

For convenience, cf.TtimeDuration instances can be created with the following constructors:

Constructor	Description
cf.Y	A cf.TimeDuration object for a number of calendar years
cf.M	A cf.TimeDuration object for a number of calendar months
cf.D	A cf.TimeDuration object for a number of days
cf.h	A cf.TimeDuration object for a number of hours
cf.m	A cf.TimeDuration object for a number of minutes
cf.s	A cf.TimeDuration object for a number of seconds

Some examples of ‘cf.TimeDuration’ objects returned by constructors.

>>> cf.D()
<CF TimeDuration: P1D (Y-M-D 00:00:00)>
>>> cf.Y(10, month=12)
<CF TimeDuration: P10Y (Y-12-01 00:00:00)>

----

Domain

The domain of the CF data model is not a construct, but is defined collectively by various other metadata constructs included in the field construct. It is represented by the cf.Domain class. The domain instance may be accessed with the domain attribute, or get_domain method, of the field construct.

Get the domain, and inspect it.

>>> domain = t.domain
>>> domain
<CF Domain: {1, 1, 9, 10}>
>>> print(domain)
Dimension coords: atmosphere_hybrid_height_coordinate(1) = [1.5]
                : grid_latitude(10) = [2.2, ..., -1.76] degrees
                : grid_longitude(9) = [-4.7, ..., -1.18] degrees
                : time(1) = [2019-01-01 00:00:00]
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[53.941, ..., 50.225]] degrees_N
                : longitude(grid_longitude(9), grid_latitude(10)) = [[2.004, ..., 8.156]] degrees_E
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., 'kappa']
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[2391.9657, ..., 2392.6009]] km2
Coord references: grid_mapping_name:rotated_latitude_longitude
                : standard_name:atmosphere_hybrid_height_coordinate
Domain ancils   : ncvar%a(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
                : ncvar%b(atmosphere_hybrid_height_coordinate(1)) = [20.0]
                : surface_altitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 270.0]] m
>>> description = domain.dump(display=False)

Changes to domain instance are seen by the field construct, and vice versa. This is because the domain instance is merely a “view” of the relevant metadata constructs contained in the field construct.

Change a property of a metadata construct of the domain and show that this change appears in the same metadata data construct of the parent field, and vice versa.

>>> domain_latitude = t.domain.constructs('latitude').value()
>>> field_latitude = t.constructs('latitude').value()
>>> domain_latitude.set_property('test', 'set by domain')
>>> print(field_latitude.get_property('test'))
set by domain
>>> field_latitude.set_property('test', 'set by field')
>>> print(domain_latitude.get_property('test'))
set by field
>>> domain_latitude.del_property('test')
'set by field'
>>> field_latitude.has_property('test')
False

All of the methods and attributes related to the domain are listed here.

---

Metadata construct types

Domain axes

A domain axis metadata construct specifies the number of points along an independent axis of the field construct’s domain and is stored in a cf.DomainAxis instance. The size of the axis is retrieved with the get_size method of the domain axis construct.

Get the size of a domain axis construct.

>>> print(q.domain_axes)
Constructs:
{'domainaxis0': <CF DomainAxis: size(5)>,
 'domainaxis1': <CF DomainAxis: size(8)>,
 'domainaxis2': <CF DomainAxis: size(1)>}
>>> d = q.domain_axes.get('domainaxis1')
>>> d
<CF DomainAxis: size(8)>
>>> d.get_size()
8

Coordinates

There are two types of coordinate construct, dimension and auxiliary coordinate constructs, which can be retrieved together with the coordinates method of the field construct, as well as individually with the auxiliary_coordinates and dimension_coordinates methods.

Retrieve both types of coordinate constructs.

>>> print(t.coordinates)
Constructs:
{'auxiliarycoordinate0': <CF AuxiliaryCoordinate: latitude(10, 9) degrees_N>,
 'auxiliarycoordinate1': <CF AuxiliaryCoordinate: longitude(9, 10) degrees_E>,
 'auxiliarycoordinate2': <CF AuxiliaryCoordinate: long_name=Grid latitude name(10) >,
 'dimensioncoordinate0': <CF DimensionCoordinate: atmosphere_hybrid_height_coordinate(1) >,
 'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>,
 'dimensioncoordinate2': <CF DimensionCoordinate: grid_longitude(9) degrees>,
 'dimensioncoordinate3': <CF DimensionCoordinate: time(1) days since 2018-12-01 >}

Bounds

A coordinate construct may contain an array of cell bounds that provides the extent of each cell by defining the locations of the cell vertices. This is in addition to the main data array that contains a grid point location for each cell. The cell bounds are stored in a cf.Bounds class instance that is accessed with the bounds attribute, or get_bounds method, of the coordinate construct.

A cf.Bounds instance shares the the same API as the field construct for accessing its data.

Get the Bounds instance of a coordinate construct and inspect its data.

>>> lon = t.constructs('grid_longitude').value()
>>> bounds = lon.bounds
>>> bounds
<CF Bounds: grid_longitude(9, 2) degrees>
>>> bounds.data
<CF Data(9, 2): [[-4.92, ..., -0.96]] degrees>
>>> print(bounds.array)
[[-4.92 -4.48]
 [-4.48 -4.04]
 [-4.04 -3.6 ]
 [-3.6  -3.16]
 [-3.16 -2.72]
 [-2.72 -2.28]
 [-2.28 -1.84]
 [-1.84 -1.4 ]
 [-1.4  -0.96]]

The cf.Bounds instance inherits the descriptive properties from its parent coordinate construct, but it may also have its own properties (although setting these is not recommended).

Inspect the inherited and bespoke properties of a Bounds instance.

>>> bounds.inherited_properties()
{'standard_name': 'grid_longitude',
 'units': 'degrees'}
>>> bounds.properties()
{'units': 'degrees'}

Geometry cells

For many geospatial applications, cell bounds can not be represented by a simple line or polygon, and different cells may have different numbers of nodes describing their bounds. For example, if each cell describes the areal extent of a watershed, then it is likely that some watersheds will require more nodes than others. Such cells are called geometries.

If a coordinate construct represents geometries then it will have a “geometry” attribute (not a CF property) with one of the values 'point', ‘line' or 'polygon'.

This is illustrated with the file geometry.nc (found in the sample datasets):

Read and inspect a dataset containing geometry cell bounds.

>>> f = cf.read('geometry.nc')[0]
>>> print(f)
Field: preciptitation_amount (ncvar%pr)
---------------------------------------
Data            : preciptitation_amount(cf_role=timeseries_id(2), time(4))
Dimension coords: time(4) = [2000-01-02 00:00:00, ..., 2000-01-05 00:00:00]
Auxiliary coords: latitude(cf_role=timeseries_id(2)) = [25.0, 7.0] degrees_north
                : longitude(cf_role=timeseries_id(2)) = [10.0, 40.0] degrees_east
                : altitude(cf_role=timeseries_id(2)) = [5000.0, 20.0] m
                : cf_role=timeseries_id(cf_role=timeseries_id(2)) = [b'x1', b'y2']
Coord references: grid_mapping_name:latitude_longitude
>>> lon = f.auxiliary_coordinate('X')
>>> lon.dump()
Auxiliary coordinate: longitude
   standard_name = 'longitude'
   units = 'degrees_east'
   Data(2) = [10.0, 40.0] degrees_east
   Geometry: polygon
   Bounds:axis = 'X'
   Bounds:standard_name = 'longitude'
   Bounds:units = 'degrees_east'
   Bounds:Data(2, 3, 4) = [[[20.0, ..., --]]] degrees_east
   Interior Ring:Data(2, 3) = [[0, ..., --]]
>>> lon.get_geometry()
'polygon'

Bounds for geometry cells are also stored in a Bounds instance, but one that always has two extra trailing dimensions (rather than one). The fist trailing dimension indexes the distinct parts of a geometry, and the second indexes the nodes of each part. When a part has fewer nodes than another, its nodes dimension is padded with missing data.

Inspect the geometry nodes.

>>> print(lon.bounds.data.array)
[[20.0 10.0  0.0   --]
 [ 5.0 10.0 15.0 10.0]
 [20.0 10.0  0.0   --]]

[[50.0 40.0 30.0   --]
 [  --   --   --   --]
 [  --   --   --   --]]]

If a cell is composed of multiple polygon parts, an individual polygon may define an “interior ring”, i.e. a region that is to be omitted from, as opposed to included in, the cell extent. Such cells also have an interior ring array that spans the same domain axes as the coordinate cells, with the addition of one extra dimension that indexes the parts for each cell. This array records whether each polygon is to be included or excluded from the cell, with vlaues of 1 or 0 respectively.

Inspect the interior ring information.

>>> print(lon.get_interior_ring().data.array)
[[0  1  0]
 [0 -- --]]

Note it is preferable to access the data type, number of dimensions, dimension sizes and number of elements of the coordinate construct via the construct’s attributes, rather than the attributes of the cf.Data instance that provides representative values for each cell. This is because the representative cell values for geometries are optional, and if they are missing then the construct attributes are able to infer these attributes from the bounds.

When a field construct containing geometries is written to disk, a CF-netCDF geometry container variable is automatically created, and the cells encoded with the compression techniques defined in the CF conventions.

Domain ancillaries

A domain ancillary construct provides information which is needed for computing the location of cells in an alternative coordinate system. If a domain ancillary construct provides extra coordinates then it may contain cell bounds in addition to its main data array.

Get the data and bounds data of a domain ancillary construct.

>>> a = t.constructs.get('domainancillary0')
>>> print(a.array)
[10.]
>>> bounds = a.bounds
>>> bounds
<Bounds: ncvar%a_bounds(1, 2) m>
>>> print(bounds.array)
[[  5.  15.]]

Coordinate systems

A field construct may contain various coordinate systems. Each coordinate system is either defined by a coordinate reference construct that relates dimension coordinate, auxiliary coordinate and domain ancillary constructs (as is the case for the field construct t), or is inferred from dimension and auxiliary coordinate constructs alone (as is the case for the field construct q).

A coordinate reference construct contains

• references (by construct keys) to the dimension and auxiliary coordinate constructs to which it applies, accessed with the coordinates method of the coordinate reference construct;

• the zeroes of the dimension and auxiliary coordinate constructs which define the coordinate system, stored in a cf.Datum instance, which is accessed with the datum attribute, or get_datum method, of the coordinate reference construct; and

• a formula for converting coordinate values taken from the dimension or auxiliary coordinate constructs to a different coordinate system, stored in a cf.CoordinateConversion class instance, which is accessed with the coordinate_conversion attribute, or get_coordinate_conversion method, of the coordinate reference construct.

Select the vertical coordinate system construct and inspect its coordinate constructs.

>>> crs = t.constructs('standard_name:atmosphere_hybrid_height_coordinate').value()
>>> crs
<CF CoordinateReference: standard_name:atmosphere_hybrid_height_coordinate>
>>> crs.dump()
Coordinate Reference: atmosphere_hybrid_height_coordinate
    Coordinate conversion:computed_standard_name = altitude
    Coordinate conversion:standard_name = atmosphere_hybrid_height_coordinate
    Coordinate conversion:a = domainancillary0
    Coordinate conversion:b = domainancillary1
    Coordinate conversion:orog = domainancillary2
    Datum:earth_radius = 6371007
    Coordinate: dimensioncoordinate0
>>> crs.coordinates()
{'dimensioncoordinate0'}

Get the datum and inspect its parameters.

>>> crs.datum
<CF Datum: Parameters: earth_radius>
>>> crs.datum.parameters()
{'earth_radius': 6371007}

Get the coordinate conversion and inspect its parameters and referenced domain ancillary constructs.

>>> crs.coordinate_conversion
<CF CoordinateConversion: Parameters: computed_standard_name, standard_name; Ancillaries: a, b, orog>
>>> crs.coordinate_conversion.parameters()
{'computed_standard_name': 'altitude',
 'standard_name': 'atmosphere_hybrid_height_coordinate'}
>>> crs.coordinate_conversion.domain_ancillaries()
{'a': 'domainancillary0',
 'b': 'domainancillary1',
 'orog': 'domainancillary2'}

Cell methods

A cell method construct describes how the data represent the variation of the physical quantity within the cells of the domain and is stored in a cf.CellMethod instance. A field constructs allows multiple cell method constructs to be recorded.

Inspect the cell methods. The description follows the CF conventions for cell_method attribute strings, apart from the use of construct keys instead of netCDF variable names for cell method axes identification.

>>> print(t.cell_methods)
Constructs:
{'cellmethod0': <CF CellMethod: domainaxis1: domainaxis2: mean where land (interval: 0.1 degrees)>,
 'cellmethod1': <CF CellMethod: domainaxis3: maximum>}

The application of cell methods is not commutative (e.g. a mean of variances is generally not the same as a variance of means), so a cf.Constructs instance has an ordered method to retrieve the cell method constructs in the same order that they were were added to the field construct during field construct creation.

Retrieve the cell method constructs in the same order that they were applied.

>>> t.cell_methods.ordered()
OrderedDict([('cellmethod0', <CF CellMethod: domainaxis1: domainaxis2: mean where land (interval: 0.1 degrees)>),
             ('cellmethod1', <CF CellMethod: domainaxis3: maximum>)])

The axes to which the method applies, the method itself, and any qualifying properties are accessed with the get_axes, get_method, , get_qualifier and qualifiers methods of the cell method construct.

Get the domain axes constructs to which the cell method construct applies, and the method and other properties.

>>> cm = t.constructs('method:mean').value()
>>> cm
<CF CellMethod: domainaxis1: domainaxis2: mean where land (interval: 0.1 degrees)>
>>> cm.get_axes()
('domainaxis1', 'domainaxis2')
>>> cm.get_method()
'mean'
>>> cm.qualifiers()
{'where': 'land', 'interval': [<CF Data(): 0.1 degrees>]}
>>> cm.get_qualifier('where')
'land'

Field ancillaries

A field ancillary construct provides metadata which are distributed over the same domain as the field construct itself. For example, if a field construct holds a data retrieved from a satellite instrument, a field ancillary construct might provide the uncertainty estimates for those retrievals (varying over the same spatiotemporal domain).

Get the properties and data of a field ancillary construct.

>>> a = t.get_construct('fieldancillary0')
>>> a
<CF FieldAncillary: air_temperature standard_error(10, 9) K>
>>> a.properties()
{'standard_name': 'air_temperature standard_error',
 'units': 'K'}
>>> a.data
<CF Data(10, 9): [[0.76, ..., 0.32]] K>

---

Cyclic domain axes

A domain axis is cyclic if cells at both of its ends are actually geographically adjacent. For example, a longitude cell spanning 359 to 360 degrees east is adjacent to the cell spanning 0 to 1 degrees east.

When a dimension coordinate construct is set on a field construct, the cyclicity of its dimension is automatically determined, using the autocyclic method of the field construct, provided the field construct has sufficient coordinate metadata for it to be inferred.

To find out whether a dimension is cyclic use the iscyclic method of the field construct, or to manually set its cyclicity use the cyclic method.

Cyclicity is used by subspacing and mathematical operations to “wrap” cyclic dimensions to give appropriate results.

Rolling a cyclic axis

The field construct may be “rolled” along a cyclic axis with the roll method of the field construct. This means that the data along that axis so that a given number of elements from one edge of the dimension are removed and re-introduced at the other edge. All metadata constructs whose data spans the cyclic axis are also rolled.

Roll the data along the ‘X’ axis one element to the right, and also three elements to the left.

>>> print(q.array[0])
[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
>>> print(q.roll('X', shift=1).array[0])
[0.029 0.007 0.034 0.003 0.014 0.018 0.037 0.024]
>>> qr = q.roll('X', shift=-3)
>>> print(qr.array[0])
[0.014 0.018 0.037 0.024 0.029 0.007 0.034 0.003]

Inspect the ‘X’ dimension coordinates of the original and rolled field constructs, showing that monotonicity has been preserved.

>>> print(q.dimension_coordinate('X').array)
[ 22.5  67.5 112.5 157.5 202.5 247.5 292.5 337.5]
>>> print(qr.dimension_coordinate('X').array)
[-202.5 -157.5 -112.5  -67.5  -22.5   22.5   67.5  112.5]

Anchoring a cyclic axis

The field construct may be rolled by specifying a dimension coordinate value that should be contained in the first element of the data for the corresponding axis, by specifying the coordinate value via the anchor method if the field construct.

Roll the data along the ‘X’ axis so that the first element of the axis contains 200 degrees east, and also -750 degrees east.

>>> print(q.anchor('X', -150))
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [-112.5, ..., 202.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(q.anchor('X', -750))
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [-742.5, ..., -427.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]

---

Subspacing by metadata

Creation of a new field construct which spans a subspace of the domain of an existing field construct is achieved either by indexing the field construct directly (see Subspacing by index) or by identifying indices based on the metadata constructs (as described in this section). The subspacing operation, in either case, also subspaces any metadata constructs of the field construct (e.g. coordinate metadata constructs) which span any of the domain axis constructs that are affected. The new field construct is created with the same properties as the original field construct.

Subspacing by metadata uses the subspace method of the field construct to select metadata constructs and specify conditions on their data. Indices for subspacing are then automatically inferred from where the conditions are met.

Metadata constructs and the conditions on their data are defined by keyword parameters to the subspace method. A keyword name is an identity of a metadata construct, and the keyword value provides a condition for inferring indices that apply to the dimension (or dimensions) spanned by the metadata construct’s data. Indices are created that select every location for which the metadata construct’s data satisfies the condition.

Create a new field construct whose ‘X’ coordinate spans only 112.5 degrees east, with the other domain axes remaining unchanged.

>>> print(q)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01T00:00:00Z]
>>> print(q.construct('X').array)
[ 22.5  67.5 112.5 157.5 202.5 247.5 292.5 337.5]
>>> q2 = q.subspace(X=112.5)
>>> print(q2)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(1)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(1) = [112.5] degrees_east
                : time(1) = [2019-01-01T00:00:00Z]

Any domain axes that have not been identified remain unchanged.

Multiple domain axes may be subspaced simultaneously, and it doesn’t matter which order they are specified in the subspace call.

Create a new field construct whose domain spans only 112.5 degrees east and has latitude greater than -60 degrees north, with the other domain axes remaining unchanged.

>>> print(q.construct('latitude').array)
[-75. -45.   0.  45.  75.]
>>> print(q.subspace(X=112.5, latitude=cf.gt(-60)))
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(4), longitude(1)) 1
Cell methods    : area: mean
Dimension coords: latitude(4) = [-45.0, ..., 75.0] degrees_north
                : longitude(1) = [112.5] degrees_east
                : time(1) = [2019-01-01T00:00:00Z]

In the above example, cf.gt(-60) returns a cf.Query instance which defines a condition (“greater than -60”) that can be applied to the selected construct’s data. See Encapsulating conditions for details.

Create a new field construct whose domain spans only 45 degrees south and latitudes greater than 20 degrees north.

>>> c = cf.eq(-45) | cf.ge(20)
>>> c
<CF Query: [(eq -45) | (ge 20)]>
>>> print(q.subspace(latitude=c))
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(3), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(3) = [-45.0, 45.0, 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01T00:00:00Z]

In the above example, two cf.Query instances are combined into a new cf.Query instance via the Python bitwise “or” operator (|). See Encapsulating conditions for details.

Subspace criteria may be provided for size 1 domain axes that are not spanned by the field construct’s data.

Explicit indices may also be assigned to a domain axis identified by a metadata construct, with either a Python slice object, or a sequence of integers or booleans.

Create a new field construct whose domain spans the 2nd, 3rd and 5th elements of the ‘X’ axis, and reverses the ‘Y’ axis.

>>> print(q.subspace(X=[1, 2, 4], Y=slice(None, None, -1)))
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(3)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [75.0, ..., -75.0] degrees_north
                : longitude(3) = [67.5, 112.5, 202.5] degrees_east
                : time(1) = [2019-01-01T00:00:00Z]

For a dimension that is cyclic, a subspace defined by a slice or by a cf.Query instance is assumed to “wrap” around the edges of the data.

Create subspaces that wrap around a cyclic dimension.

>>> print(q.subspace(X=cf.wi(-100, 200)))
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(6)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(6) = [-67.5, ..., 157.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print (q.subspace(X=slice(-2, 4)))
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(6)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(6) = [-67.5, ..., 157.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]

Susbaces in time

Subspaces based on time dimensions may be defined with as elapsed times since the reference date, or with date-time objects.

Create a new field construct whose domain’s time axis contains a single cell for 2019-01-01. TODO

>>> a = cf.read('timeseries.nc')[0]
>>> print (a)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(5), longitude(8)) K
Cell methods    : area: mean
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(a.coordinate('T').array[0:9])
[349.5 380.5 410.5 440.5 471.  501.5 532.  562.5 593.5]
>>> print(a.coordinate('T').datetime_array[0:9])
[cftime.DatetimeGregorian(1959-12-16 12:00:00)
 cftime.DatetimeGregorian(1960-01-16 12:00:00)
 cftime.DatetimeGregorian(1960-02-15 12:00:00)
 cftime.DatetimeGregorian(1960-03-16 12:00:00)
 cftime.DatetimeGregorian(1960-04-16 00:00:00)
 cftime.DatetimeGregorian(1960-05-16 12:00:00)
 cftime.DatetimeGregorian(1960-06-16 00:00:00)
 cftime.DatetimeGregorian(1960-07-16 12:00:00)
 cftime.DatetimeGregorian(1960-08-16 12:00:00)]
>>> print(a.subspace(T=410.5))
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(1), latitude(5), longitude(8)) K
Cell methods    : area: mean
Dimension coords: time(1) = [1960-02-15 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(a.subspace(T=cf.dt('1960-04-16')))
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(1), latitude(5), longitude(8)) K
Cell methods    : area: mean
Dimension coords: time(1) = [1960-04-16 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(a.subspace(T=cf.wi(cf.dt('1962-11-01'), cf.dt('1967-03-17 07:30'))))
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(53), latitude(5), longitude(8)) K
Cell methods    : area: mean
Dimension coords: time(53) = [1962-11-16 00:00:00, ..., 1967-03-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa

Subspace mode

There are three modes of operation, each of which provides a different type of subspace:

• compress mode. This is the default mode. Unselected locations are removed to create the returned subspace:

  Create TODO

  >>> print(q.array)
  [[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
   [0.023 0.036 0.045 0.062 0.046 0.073 0.006 0.066]
   [0.11  0.131 0.124 0.146 0.087 0.103 0.057 0.011]
   [0.029 0.059 0.039 0.07  0.058 0.072 0.009 0.017]
   [0.006 0.036 0.019 0.035 0.018 0.037 0.034 0.013]]
  >>> q2 = q.subspace('compress', X=[1, 2, 4, 6])
  >>> print(q2)
  Field: specific_humidity (ncvar%q)
  ----------------------------------
  Data            : specific_humidity(latitude(5), longitude(4)) 1
  Cell methods    : area: mean
  Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                  : longitude(4) = [67.5, ..., 292.5] degrees_east
                  : time(1) = [2019-01-01T00:00:00Z]
  
  >>> print(q2.array)
  [[0.034 0.003 0.018 0.024]
   [0.036 0.045 0.046 0.006]
   [0.131 0.124 0.087 0.057]
   [0.059 0.039 0.058 0.009]
   [0.036 0.019 0.018 0.034]]
  

  Note that if a multi-dimensional metadata construct is being used to define the indices then some missing data may still be inserted at unselected locations.

• envelope mode. The returned subspace is the smallest that contains all of the selected indices. Missing data is inserted at unselected locations within the envelope.

  Create TODO

  >>> q2 = q.subspace('envelope', X=[1, 2, 4, 6])
  >>> print(q2)
  Field: specific_humidity (ncvar%q)
  ----------------------------------
  Data            : specific_humidity(latitude(5), longitude(6)) 1
  Cell methods    : area: mean
  Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                  : longitude(4) = [67.5, ..., 292.5] degrees_east
                  : time(1) = [2019-01-01T00:00:00Z]
  >>> print(q2.array)
  [[0.034 0.003 -- 0.018 -- 0.024]
   [0.036 0.045 -- 0.046 -- 0.006]
   [0.131 0.124 -- 0.087 -- 0.057]
   [0.059 0.039 -- 0.058 -- 0.009]
   [0.036 0.019 -- 0.018 -- 0.034]]
  

• full mode. The returned subspace has the same domain as the original field construct. Missing data is inserted at unselected locations.

  Create TODO

  >>> q2 = q.subspace('full', X=[1, 2, 4, 6])
  >>> print(q2)
  Field: specific_humidity (ncvar%q)
  ----------------------------------
  Data            : specific_humidity(latitude(5), longitude(8)) 1
  Cell methods    : area: mean
  Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                  : longitude(8) = [22.5, ..., 337.5] degrees_east
                  : time(1) = [2019-01-01T00:00:00Z]
  
  >>> print(q2.array)
  [[-- 0.034 0.003 -- 0.018 -- 0.024 --]
   [-- 0.036 0.045 -- 0.046 -- 0.006 --]
   [-- 0.131 0.124 -- 0.087 -- 0.057 --]
   [-- 0.059 0.039 -- 0.058 -- 0.009 --]
   [-- 0.036 0.019 -- 0.018 -- 0.034 --]]
  

The where method of the field construct also allows values (including missing data) to be assigned to the data based on criteria applying to the field construct’s data, its metadata constructs; or inserted from another field construct. See Assignment by condition.

Multiple dimensions

Conditions may also be applied to multi-dimensionsal metadata constructs

Create TODO

>>> print(t)
Field: air_temperature (ncvar%ta)
---------------------------------
Data            : air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
Cell methods    : grid_latitude(10): grid_longitude(9): mean where land (interval: 0.1 degrees) time(1): maximum
Field ancils    : air_temperature standard_error(grid_latitude(10), grid_longitude(9)) = [[0.81, ..., 0.78]] K
Dimension coords: time(1) = [2019-01-01 00:00:00]
                : atmosphere_hybrid_height_coordinate(1) = [1.5]
                : grid_latitude(10) = [2.2, ..., -1.76] degrees
                : grid_longitude(9) = [-4.7, ..., -1.18] degrees
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[53.941, ..., 50.225]] degrees_N
                : longitude(grid_longitude(9), grid_latitude(10)) = [[2.004, ..., 8.156]] degrees_E
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., 'kappa']
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[2391.9657, ..., 2392.6009]] km2
Coord references: grid_mapping_name:rotated_latitude_longitude
                : standard_name:atmosphere_hybrid_height_coordinate
Domain ancils   : ncvar%a(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
                : ncvar%b(atmosphere_hybrid_height_coordinate(1)) = [20.0]
                : surface_altitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 270.0]] m
>>> print(t.construct('latitude').array)
[[53.941 53.987 54.029 54.066 54.099 54.127 54.15  54.169 54.184]
 [53.504 53.55  53.591 53.627 53.66  53.687 53.711 53.729 53.744]
 [53.067 53.112 53.152 53.189 53.221 53.248 53.271 53.29  53.304]
 [52.629 52.674 52.714 52.75  52.782 52.809 52.832 52.85  52.864]
 [52.192 52.236 52.276 52.311 52.343 52.37  52.392 52.41  52.424]
 [51.754 51.798 51.837 51.873 51.904 51.93  51.953 51.971 51.984]
 [51.316 51.36  51.399 51.434 51.465 51.491 51.513 51.531 51.545]
 [50.879 50.922 50.96  50.995 51.025 51.052 51.074 51.091 51.105]
 [50.441 50.484 50.522 50.556 50.586 50.612 50.634 50.652 50.665]
 [50.003 50.045 50.083 50.117 50.147 50.173 50.194 50.212 50.225]]
>>> t2 = t.subspace(latitude=cf.wi(51, 53))
>>> print(t2.array)
[[[261.7 260.6 270.8 260.3 265.6 279.4 276.9 267.6 260.6]
  [264.2 275.9 262.5 264.9 264.7 270.2 270.4 268.6 275.3]
  [263.9 263.8 272.1 263.7 272.2 264.2 260.0 263.5 270.2]
  [273.8 273.1 268.5 272.3 264.3 278.7 270.6 273.0 270.6]
  [   --    --    --    -- 261.2 275.3 271.2 260.8 268.9]]]

The “compress” mode is still the default mode, but because the indices may not be acting along orthogonal dimensions, some missing data may still need to be inserted into the field construct’s data, as is the case in this example.

Assignment by metadata

Data elements can be changed by assigning to elements selected by indices of the data (see Assignment by index); by conditions based on the data values of the field construct or one if its metadata constructs (see Assignment by condition); or by identifying indices based on arbitrary metadata constructs (as described in this section).

Assignment by metadata makes use of the indices method of the field construct to select metadata constructs and specify conditions on their data. Indices for subspacing are then automatically inferred from where the conditions are met. The tuple of indices returned by the indices may the be used in normal assignment by index.

The indices method takes exactly the same arguments as the subspace method of the field construct. See Subspacing by metadata for details.

Create TODO

>>> q, t = cf.read('file.nc')
>>> print(t)
Field: air_temperature (ncvar%ta)
---------------------------------
Data            : air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
Cell methods    : grid_latitude(10): grid_longitude(9): mean where land (interval: 0.1 degrees) time(1): maximum
Field ancils    : air_temperature standard_error(grid_latitude(10), grid_longitude(9)) = [[0.76, ..., 0.32]] K
Dimension coords: atmosphere_hybrid_height_coordinate(1) = [1.5]
                : grid_latitude(10) = [2.2, ..., -1.76] degrees
                : grid_longitude(9) = [-4.7, ..., -1.18] degrees
                : time(1) = [2019-01-01 00:00:00]
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[53.941, ..., 50.225]] degrees_N
                : longitude(grid_longitude(9), grid_latitude(10)) = [[2.004, ..., 8.156]] degrees_E
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., b'kappa']
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[2391.9657, ..., 2392.6009]] km2
Coord references: grid_mapping_name:rotated_latitude_longitude
                : standard_name:atmosphere_hybrid_height_coordinate
Domain ancils   : ncvar%a(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
                : ncvar%b(atmosphere_hybrid_height_coordinate(1)) = [20.0]
                : surface_altitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 270.0]] m
>>> indices = t.indices(grid_longitude=cf.wi(-4, -2))
>>> indices
(slice(0, 1, 1), slice(0, 10, 1), slice(2, 7, 1))
>>> t[indices] = -11
>>> print(t.array)
[[[262.8 270.5 -11.  -11.  -11.  -11.  -11.  278.9 269.2]
  [272.7 268.4 -11.  -11.  -11.  -11.  -11.  265.7 279.5]
  [269.7 279.1 -11.  -11.  -11.  -11.  -11.  272.5 263.7]
  [261.7 260.6 -11.  -11.  -11.  -11.  -11.  267.6 260.6]
  [264.2 275.9 -11.  -11.  -11.  -11.  -11.  268.6 275.3]
  [263.9 263.8 -11.  -11.  -11.  -11.  -11.  263.5 270.2]
  [273.8 273.1 -11.  -11.  -11.  -11.  -11.  273.  270.6]
  [267.9 273.5 -11.  -11.  -11.  -11.  -11.  260.8 268.9]
  [270.9 278.7 -11.  -11.  -11.  -11.  -11.  278.5 266.4]
  [276.4 264.2 -11.  -11.  -11.  -11.  -11.  273.4 269.7]]]
>>> t[t.indices(latitude=cf.wi(51, 53))] = -99
>>> print(t.array)
[[[262.8 270.5 -11.  -11.  -11.  -11.  -11.  278.9 269.2]
  [272.7 268.4 -11.  -11.  -11.  -11.  -11.  265.7 279.5]
  [269.7 279.1 -11.  -11.  -11.  -11.  -11.  272.5 263.7]
  [-99.  -99.  -99.  -99.  -99.  -99.  -99.  -99.  -99. ]
  [-99.  -99.  -99.  -99.  -99.  -99.  -99.  -99.  -99. ]
  [-99.  -99.  -99.  -99.  -99.  -99.  -99.  -99.  -99. ]
  [-99.  -99.  -99.  -99.  -99.  -99.  -99.  -99.  -99. ]
  [267.9 273.5 -11.  -11.  -99.  -99.  -99.  -99.  -99. ]
  [270.9 278.7 -11.  -11.  -11.  -11.  -11.  278.5 266.4]
  [276.4 264.2 -11.  -11.  -11.  -11.  -11.  273.4 269.7]]]

---

Sorting and selecting from field lists

A field list may be sorted in-place using the same syntax as a Python list. By default the field list is sorted by the values of the field constructs identities, but any sorting criteria are possible.

Sort a field list by the field construct identities, and by field construct units.

>>> fl = cf.read('file.nc')
>>> fl
[<CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>]
>>> fl.sort()
>>> fl
[<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>,
 <CF Field: specific_humidity(latitude(5), longitude(8)) 1>]
>>> fl.sort(key=lambda f: f.units)
>>> fl
[<CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>]

A field list has methods for selecting field constructs that meet various criteria:

Method	Filter criteria
select_by_identity	Field construct identity
select_by_property	Property values
select_by_units	Units values.
select_by_rank	The total number of domain axis constructs in the domain
select_by_naxes	The number of domain axis constructs spanned by the data
select_by_construct	Existence and values of metadata constructs
select_by_ncvar	NetCDF variable name (see the netCDF interface)

Each of these methods returns a new (possibly empty) field list that contains the selected field constructs.

Get field constructs by their identity.

>>> fl = cf.read('*.nc')
>>> fl
[<CF Field: specific_humidity(cf_role=timeseries_id(4), ncdim%timeseries(9))>,
 <CF Field: eastward_wind(latitude(10), longitude(9)) m s-1>,
 <CF Field: cell_area(ncdim%longitude(9), ncdim%latitude(10)) m2>,
 <CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>,
 <CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>,
 <CF Field: air_potential_temperature(time(120), latitude(5), longitude(8)) K>,
 <CF Field: precipitation_flux(time(2), latitude(4), longitude(5)) kg m2 s-1>,
 <CF Field: precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1>]
>>> fl.select_by_identity('precipitation_flux')
[<CF Field: precipitation_flux(time(2), latitude(4), longitude(5)) kg m2 s-1>,
 <CF Field: precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1>]
>>> import re
>>> fl.select_by_identity(re.compile('.*potential.*'))
[<CF Field: air_potential_temperature(time(120), latitude(5), longitude(8)) K>]
>>> fl.select_by_identity('relative_humidity')
[]

As a convenience, selection by field construct identity is also possible by providing identities to a call of a field list itself, or to its select method.

Get field constructs by their identity by calling the instance directly, or with the ‘select’ method.

>>> fl('air_temperature')
[<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>,
 <CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>]
>>> fl.select('air_temperature')
[<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>,
 <CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>]

Testing criteria on a field construct

A field construct has methods for ascertaining whether or not it meets various criteria:

Method	Match criteria
match_by_identity	Field construct identity
match	Field construct identity
match_by_property	Property values
match_by_units	Units values.
match_by_rank	The total number of domain axis constructs in the domain
match_by_naxes	The number of domain axis constructs spanned by the data
match_by_construct	Existence and values of metadata constructs
match_by_ncvar	NetCDF variable name (see the netCDF interface)

Each of these methods returns True if the field construct matches the given criteria, or else False.

Match a field construct to its properties and metadata.

>>> print(t)
Field: air_temperature (ncvar%ta)
---------------------------------
Data            : air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
Cell methods    : grid_latitude(10): grid_longitude(9): mean where land (interval: 0.1 degrees) time(1): maximum
Field ancils    : air_temperature standard_error(grid_latitude(10), grid_longitude(9)) = [[0.76, ..., 0.32]] K
Dimension coords: atmosphere_hybrid_height_coordinate(1) = [1.5]
                : grid_latitude(10) = [2.2, ..., -1.76] degrees
                : grid_longitude(9) = [-4.7, ..., -1.18] degrees
                : time(1) = [2019-01-01 00:00:00]
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[53.941, ..., 50.225]] degrees_N
                : longitude(grid_longitude(9), grid_latitude(10)) = [[2.004, ..., 8.156]] degrees_E
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., 'kappa']
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[2391.9657, ..., 2392.6009]] km2
Coord references: grid_mapping_name:rotated_latitude_longitude
                : standard_name:atmosphere_hybrid_height_coordinate
Domain ancils   : ncvar%a(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
                : ncvar%b(atmosphere_hybrid_height_coordinate(1)) = [20.0]
                : surface_altitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 270.0]] m
>>> t.match_by_identity('air_temperature')
True
>>> t.match_by_rank(4)
True
>>> t.match_by_units('degC', exact=False)
True
>>> t.match_by_construct(longitude=cf.wi(-10, 10))
True

As a convenience, matching a field construct by identity is also possible with the match method, which is as alias for match_by_identity.

Match a field construct to its identity.

>>> t.match('specific_humidity')
False
>>> t.match('specific_humidity', 'air_temperature')
True

---

Encapsulating conditions

A condition that may be applied to any construct (or, indeed, any object) may be stored in a cf.Query object. A cf.Query object encapsulates a condition, such as “strictly less than 3”. When applied to an object, via the cf.Query instance’s evaluate method or the Python equality (==) operator, the condition is evaluated in the context of that object.

TODO

>>> c = cf.Query('lt', 3)
>>> c
<CF Query: (lt 3)>
>>> c.evaluate(2)
True
>>> c == 2
True
>>> c != 2
False
>>> c.evaluate(3)
False
>>> c == cf.Data([1, 2, 3])
<CF Data(3): [True, True, False]>
>>> print(c == numpy.array([1, 2, 3]))
[ True  True False]

The following operators are supported when constructing cf.Query instances:

Operator	Description
'lt'	A “strictly less than” condition
'le'	A “less than or equal” condition
'gt'	A “strictly greater than” condition
'ge'	A “greater than or equal” condition
'eq'	An “equal” condition
'ne'	A “not equal” condition
'wi'	A “within a range” condition
'wo'	A “without a range” condition
'set'	A “member of set” condition

Compound conditions

Multiple conditions may be combined with the Python bitwise “and” (&) and “or” (|) operators to form a new, compound cf.Query object.

TODO

>>> ge3 = cf.Query('ge', 3)
>>> lt5 = cf.Query('lt', 5)
>>> c = ge3 & lt5
>>> c
<CF Query: [(ge 3) & (lt 5)]>
>>> c == 2
False
>>> c != 2
True
>>> c = ge3 | lt5
>>> c
<CF Query: [(ge 3) | (lt 5)]>
>>> c == 2
True
>>> c &= cf.Query('set', [1, 3, 5])
>>> c
<CF Query: [[(ge 3) | (lt 5)] & (set [1, 3, 5])]>
>>> c == 2
False
>>> c == 3
True

A condition can also be applied to an attribute (as well as attributes of attributes) of an object.

Define and apply a condition that is applied to the upper bounds of a coordinate construct’s cells.

>>> upper_bounds_ge_minus4 = cf.Query('ge', -4, attr='upper_bounds')
>>> X = t.dimension_coordinate('X')
>>> X
<CF DimensionCoordinate: grid_longitude(9) degrees>
>>> print(X.bounds.array)
[[-4.92 -4.48]
 [-4.48 -4.04]
 [-4.04 -3.6 ]
 [-3.6  -3.16]
 [-3.16 -2.72]
 [-2.72 -2.28]
 [-2.28 -1.84]
 [-1.84 -1.4 ]
 [-1.4  -0.96]]
>>> print((upper_bounds_ge_minus4 == X).array)
[False False  True  True  True  True  True  True  True]

Condition constructors

For convenience, many commonly used conditions can be created with cf.Query instance constructors.

An example of a constructor (for a cell containing a value) and its equivalent construction from constructor cf.Query instances.

>>> cf.contains(4)
<CF Query: [lower_bounds(le 4) & upper_bounds(ge 4)]>
>>> cf.Query('lt', 4, attr='lower_bounds') &  cf.Query('ge', 4, attr='upper_bounds')
<CF Query: [lower_bounds(lt 4) & upper_bounds(ge 4)]>

The following cf.Query constructors are available:

General conditions
Constructor	Description
cf.lt	A cf.Query object for a “strictly less than” condition
cf.le	A cf.Query object for a “less than or equal” condition
cf.gt	A cf.Query object for a “strictly greater than” condition
cf.ge	A cf.Query object for a “strictly greater than or equal” condition
cf.eq	A cf.Query object for an “equal” condition
cf.ne	A cf.Query object for a “not equal” condition
cf.wi	A cf.Query object for a “within a range” condition
cf.wo	A cf.Query object for a “without a range” condition
cf.set	A cf.Query object for a “member of set” condition

Date-time conditions
Constructor	Description
cf.year	A cf.Query object for a “year” condition
cf.month	A cf.Query object for a “month of the year” condition
cf.day	A cf.Query object for a “day of the month” condition
cf.hour	A cf.Query object for a “hour of the day” condition
cf.minute	A cf.Query object for a “minute of the hour” condition
cf.second	A cf.Query object for a “second of the minute” condition
cf.jja	A cf.Query object for a “month of year in June, July or August” condition
cf.son	A cf.Query object for a “month of year in September, October, November” condition
cf.djf	A cf.Query object for a “month of year in December, January, February” condition
cf.mam	A cf.Query object for a “month of year in March, April, May” condition
cf.seasons	A customizable list of cf.Query objects for “seasons in a year” conditions

Coordinate cell conditions
Constructor	Description
cf.contains	A cf.Query object for a “cell contains” condition
cf.cellsize	A cf.Query object for a “cell size” condition
cf.cellgt	A cf.Query object for a “cell bounds strictly greater than” condition
cf.cellge	A cf.Query object for a “cell bounds greater than or equal” condition
cf.celllt	A cf.Query object for a “cell bounds strictly less than” condition
cf.cellle	A cf.Query object for a “cell bounds less than or equal” condition
cf.cellwi	A cf.Query object for a “cell bounds lie within range” condition
cf.cellwo	A cf.Query object for a “cell bounds lie without range” condition

Some examples of ‘cf.Query’ objects returned by constructors.

>>> cf.ge(3)
<CF Query: (ge 3)>
>>> cf.ge(cf.dt('2000-3-23'))
<CF Query: (ge 2000-03-23 00:00:00)>
>>> cf.year(1999)
<CF Query: year(eq 1999)>
>>> cf.month(cf.wi(6, 8))
<CF Query: month(wi [6, 8])>
>>> cf.jja()
<CF Query: month(wi (6, 8))>
>>> cf.contains(4)
<CF Query: [lower_bounds(le 4) & upper_bounds(ge 4)]>
>>> cf.cellsize(cf.lt(10, 'degrees'))
<CF Query: cellsize(lt 10 degrees)>

---

Assignment by condition

Data elements can be changed by assigning to elements selected by indices of the data (see Assignment by index); by conditions based on the data values of the field construct or one of its metadata constructs (as described in this section); or by identifying indices based on arbitrary metadata constructs (see Assignment by metadata).

Assignment by condition uses the where method of the field construct. This method automatically infers indices for assignment from conditions on the field construct’s data, or its metadata. In addition, different values can be assigned to where the conditions are, and are not, met

Set all data elements that are less than 273.15 to missing data.

>>> t = cf.read('file.nc')[1]
>>> print(t.array)
[[[262.8 270.5 279.8 269.5 260.9 265.  263.5 278.9 269.2]
  [272.7 268.4 279.5 278.9 263.8 263.3 274.2 265.7 279.5]
  [269.7 279.1 273.4 274.2 279.6 270.2 280.  272.5 263.7]
  [261.7 260.6 270.8 260.3 265.6 279.4 276.9 267.6 260.6]
  [264.2 275.9 262.5 264.9 264.7 270.2 270.4 268.6 275.3]
  [263.9 263.8 272.1 263.7 272.2 264.2 260.  263.5 270.2]
  [273.8 273.1 268.5 272.3 264.3 278.7 270.6 273.  270.6]
  [267.9 273.5 279.8 260.3 261.2 275.3 271.2 260.8 268.9]
  [270.9 278.7 273.2 261.7 271.6 265.8 273.  278.5 266.4]
  [276.4 264.2 276.3 266.1 276.1 268.1 277.  273.4 269.7]]]
>>> u = t.where(cf.lt(273.15), x=cf.masked)
>>> print(u.array)
[[[   --    -- 279.8    --    --    --    -- 278.9    --]
  [   --    -- 279.5 278.9    --    -- 274.2    -- 279.5]
  [   -- 279.1 273.4 274.2 279.6    -- 280.0    --    --]
  [   --    --    --    --    -- 279.4 276.9    --    --]
  [   -- 275.9    --    --    --    --    --    -- 275.3]
  [   --    --    --    --    --    --    --    --    --]
  [273.8    --    --    --    -- 278.7    --    --    --]
  [   -- 273.5 279.8    --    -- 275.3    --    --    --]
  [   -- 278.7 273.2    --    --    --    -- 278.5    --]
  [276.4    -- 276.3    -- 276.1    -- 277.0 273.4    --]]]

Set all data elements that are less than 273.15 to 0, and all other elements to 1.

>>> u = t.where(cf.lt(273.15), x=0, y=1)
>>> print(u.array)
[[[0. 0. 1. 0. 0. 0. 0. 1. 0.]
  [0. 0. 1. 1. 0. 0. 1. 0. 1.]
  [0. 1. 1. 1. 1. 0. 1. 0. 0.]
  [0. 0. 0. 0. 0. 1. 1. 0. 0.]
  [0. 1. 0. 0. 0. 0. 0. 0. 1.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [1. 0. 0. 0. 0. 1. 0. 0. 0.]
  [0. 1. 1. 0. 0. 1. 0. 0. 0.]
  [0. 1. 1. 0. 0. 0. 0. 1. 0.]
  [1. 0. 1. 0. 1. 0. 1. 1. 0.]]]

Where the data of field ‘u’ is True, multiply all elements of ‘t’ by -1, and at all other points set ‘t’ to -99.

>>> print(t.where(u, x=-t, y=-99).array)
[[[ -99.   -99.  -279.8  -99.   -99.   -99.   -99.  -278.9  -99. ]
  [ -99.   -99.  -279.5 -278.9  -99.   -99.  -274.2  -99.  -279.5]
  [ -99.  -279.1 -273.4 -274.2 -279.6  -99.  -280.   -99.   -99. ]
  [ -99.   -99.   -99.   -99.   -99.  -279.4 -276.9  -99.   -99. ]
  [ -99.  -275.9  -99.   -99.   -99.   -99.   -99.   -99.  -275.3]
  [ -99.   -99.   -99.   -99.   -99.   -99.   -99.   -99.   -99. ]
  [-273.8  -99.   -99.   -99.   -99.  -278.7  -99.   -99.   -99. ]
  [ -99.  -273.5 -279.8  -99.   -99.  -275.3  -99.   -99.   -99. ]
  [ -99.  -278.7 -273.2  -99.   -99.   -99.   -99.  -278.5  -99. ]
  [-276.4  -99.  -276.3  -99.  -276.1  -99.  -277.  -273.4  -99. ]]]

The where method also allows the condition to be applied to a metadata construct’s data:

Where the ‘Y’ coordinates are greater than 0.5, set the field construct data to missing data.

>>> print(t.where(cf.gt(0.5), x=cf.masked, construct='grid_latitude').array)
[[[   --    --    --    --    --    --    --    --    --]
  [   --    --    --    --    --    --    --    --    --]
  [   --    --    --    --    --    --    --    --    --]
  [   --    --    --    --    --    --    --    --    --]
  [264.2 275.9 262.5 264.9 264.7 270.2 270.4 268.6 275.3]
  [263.9 263.8 272.1 263.7 272.2 264.2 260.0 263.5 270.2]
  [273.8 273.1 268.5 272.3 264.3 278.7 270.6 273.0 270.6]
  [267.9 273.5 279.8 260.3 261.2 275.3 271.2 260.8 268.9]
  [270.9 278.7 273.2 261.7 271.6 265.8 273.0 278.5 266.4]
  [276.4 264.2 276.3 266.1 276.1 268.1 277.0 273.4 269.7]]]

The hardness of the mask is respected by the where method, so missing data in the field construct can only be unmasked if the mask has first been made soft.

There are many variants on how the condition and assignment values may be specified. See the where method documentation for details.

---

Field creation

There are various methods for creating a field construct in memory:

• manual creation: Instantiate instances of field and metadata construct classes and manually provide the connections between them.

• Command modification: Produce the commands that would create an already existing field construct, and then modify them.

• Creation by conversion: Convert a single metadata construct already in memory to an independent field construct.

• Creation by reading: Create field constructs from a dataset on disk.

• Creation with the cfa command line tool: Create field constructs from existing datasets on disk.

Note that the cf package enables the creation of field constructs, but CF-compliance is the responsibility of the user. For example, a “units” property whose value is not a valid UDUNITS string is not CF-compliant, but is allowed by the cf package.

Manual creation

Manual creation of a field construct has three stages:

Stage 1: The field construct is created without metadata constructs.

Stage 2: Metadata constructs are created independently.

Stage 3: The metadata constructs are inserted into the field construct with cross-references to other, related metadata constructs if required. For example, an auxiliary coordinate construct is related to an ordered list of the domain axis constructs which correspond to its data array dimensions.

There are two equivalent approaches to stages 1 and 2.

Either as much of the content as possible is specified during object instantiation:

Create a field construct with a “standard_name” property. Create dimension coordinate and field ancillary constructs, both with properties and data.

>>> p = cf.Field(properties={'standard_name': 'precipitation_flux'})
>>> p
<CF Field: precipitation_flux>
>>> dc = cf.DimensionCoordinate(properties={'long_name': 'Longitude'},
...                               data=cf.Data([0, 1, 2.]))
>>> dc
<CF DimensionCoordinate: long_name=Longitude(3) >
>>> fa = cf.FieldAncillary(
...        properties={'standard_name': 'precipitation_flux status_flag'},
...        data=cf.Data(numpy.array([0, 0, 2], dtype='int8')))
>>> fa
<CF FieldAncillary: precipitation_flux status_flag(3) >

or else some or all content is added after instantiation via object methods:

Create empty constructs and provide them with properties and data after instantiation.

>>> p = cf.Field()
>>> p
<CF Field: >
>>> p.set_property('standard_name', 'precipitation_flux')
>>> p
<CF Field: precipitation_flux>
>>> dc = cf.DimensionCoordinate()
>>> dc
<CF DimensionCoordinate:  > # TODO
>>> dc.set_property('long_name', 'Longitude')
>>> dc.set_data(cf.Data([1, 2, 3.]))
>>> dc
<CF DimensionCoordinate: long_name=Longitude(3) >
>>> fa = cf.FieldAncillary(
...             data=cf.Data(numpy.array([0, 0, 2], dtype='int8')))
>>> fa
<CF FieldAncillary: (3) >
>>> fa.set_property('standard_name', 'precipitation_flux status_flag')
>>> fa
<CF FieldAncillary: precipitation_flux status_flag(3) >

For stage 3, the set_construct method of the field construct is used for setting metadata constructs and mapping data array dimensions to domain axis constructs. The domain axis constructs spanned by the data are inferred from the existing domain axis constructs, provided that there are no ambiguities (such as two dimensions of the same size), in which case they can be explicitly provided via their construct keys. This method returns the construct key for the metadata construct which can be used when other metadata constructs are added to the field (e.g. to specify which domain axis constructs correspond to a data array), or when other metadata constructs are created (e.g. to identify the domain ancillary constructs forming part of a coordinate reference construct):

Set a domain axis construct and use its construct key when setting the dimension coordinate construct. Also create a cell method construct that applies to the domain axis construct.

>>> longitude_axis = p.set_construct(cf.DomainAxis(3))
>>> longitude_axis
'domainaxis0'
>>> key = p.set_construct(dc, axes=longitude_axis)
>>> key
'dimensioncoordinate0'
>>> cm = cf.CellMethod(axes=longitude_axis, method='minimum')
>>> p.set_construct(cm)
'cellmethod0'

In general, the order in which metadata constructs are added to the field does not matter, except when one metadata construct is required by another, in which case the former must be added to the field first so that its construct key is available to the latter. Cell method constructs must, however, be set in the relative order in which their methods were applied to the data.

The domain axis constructs spanned by a metadata construct’s data may be changed after insertion with the set_data_axes method of the field construct.

Create a field construct with properties; data; and domain axis, cell method and dimension coordinate metadata constructs (data arrays have been generated with dummy values using numpy.arange).

import numpy
import cf

# Initialise the field construct with properties
Q = cf.Field(properties={'project': 'research',
                           'standard_name': 'specific_humidity',
                           'units': '1'})

# Create the domain axis constructs
domain_axisT = cf.DomainAxis(1)
domain_axisY = cf.DomainAxis(5)
domain_axisX = cf.DomainAxis(8)

# Insert the domain axis constructs into the field. The
# set_construct method returns the domain axis construct key that
# will be used later to specify which domain axis corresponds to
# which dimension coordinate construct.
axisT = Q.set_construct(domain_axisT)
axisY = Q.set_construct(domain_axisY)
axisX = Q.set_construct(domain_axisX)

# Create and insert the field construct data
data = cf.Data(numpy.arange(40.).reshape(5, 8))
Q.set_data(data)

# Create the cell method constructs
cell_method1 = cf.CellMethod(axes='area', method='mean')

cell_method2 = cf.CellMethod()
cell_method2.set_axes(axisT)
cell_method2.set_method('maximum')

# Insert the cell method constructs into the field in the same
# order that their methods were applied to the data
Q.set_construct(cell_method1)
Q.set_construct(cell_method2)

# Create a "time" dimension coordinate construct, with coordinate
# bounds
dimT = cf.DimensionCoordinate(
                            properties={'standard_name': 'time',
                                        'units': 'days since 2018-12-01'},
                            data=cf.Data([15.5]),
                            bounds=cf.Bounds(data=cf.Data([[0,31.]])))

# Create a "longitude" dimension coordinate construct, without
# coordinate bounds
dimX = cf.DimensionCoordinate(data=cf.Data(numpy.arange(8.)))
dimX.set_properties({'standard_name': 'longitude',
                     'units': 'degrees_east'})

# Create a "longitude" dimension coordinate construct
dimY = cf.DimensionCoordinate(properties={'standard_name': 'latitude',
                                          'units'        : 'degrees_north'})
array = numpy.arange(5.)
dimY.set_data(cf.Data(array))

# Create and insert the latitude coordinate bounds
bounds_array = numpy.empty((5, 2))
bounds_array[:, 0] = array - 0.5
bounds_array[:, 1] = array + 0.5
bounds = cf.Bounds(data=cf.Data(bounds_array))
dimY.set_bounds(bounds)

# Insert the dimension coordinate constructs into the field,
# specifying to which domain axis each one corresponds
Q.set_construct(dimT)
Q.set_construct(dimY)
Q.set_construct(dimX)

Inspect the new field construct.

>>> Q.dump()
------------------------
Field: specific_humidity
------------------------
project = 'research'
standard_name = 'specific_humidity'
units = '1'

Data(latitude(5), longitude(8)) = [[0.0, ..., 39.0]] 1

Cell Method: area: mean
Cell Method: time(1): maximum

Domain Axis: latitude(5)
Domain Axis: longitude(8)
Domain Axis: time(1)

Dimension coordinate: time
    standard_name = 'time'
    units = 'days since 2018-12-01'
    Data(time(1)) = [2018-12-16 12:00:00]
    Bounds:Data(time(1), 2) = [[2018-12-01 00:00:00, 2019-01-01 00:00:00]]

Dimension coordinate: latitude
    standard_name = 'latitude'
    units = 'degrees_north'
    Data(latitude(5)) = [0.0, ..., 4.0] degrees_north
    Bounds:Data(latitude(5), 2) = [[-0.5, ..., 4.5]] degrees_north

Dimension coordinate: longitude
    standard_name = 'longitude'
    units = 'degrees_east'
    Data(longitude(8)) = [0.0, ..., 7.0] degrees_east

The “Conventions” property does not need to be set because it is automatically included in output files as a netCDF global “Conventions” attribute, either as the CF version of the cf package (as returned by the cf.CF function), or else specified via the Conventions keyword of the cf.write function. See Writing to a netCDF dataset for details on how to specify additional conventions.

If this field were to be written to a netCDF dataset then, in the absence of predefined names, default netCDF variable and dimension names would be automatically generated (based on standard names where they exist). The setting of bespoke netCDF names is, however, easily done with the netCDF interface.

Set netCDF variable and dimension names for the field and metadata constructs.

Q.nc_set_variable('q')

domain_axisT.nc_set_dimension('time')
domain_axisY.nc_set_dimension('lat')
domain_axisX.nc_set_dimension('lon')

dimT.nc_set_variable('time')
dimY.nc_set_variable('lat')
dimX.nc_set_variable('lon')

Here is a more complete example which creates a field construct that contains every type of metadata construct (again, data arrays have been generated with dummy values using numpy.arange):

Create a field construct that contains at least one instance of each type of metadata construct.

import numpy
import cf

# Initialize the field construct
tas = cf.Field(
    properties={'project': 'research',
                'standard_name': 'air_temperature',
                'units': 'K'})

# Create and set domain axis constructs
axis_T = tas.set_construct(cf.DomainAxis(1))
axis_Z = tas.set_construct(cf.DomainAxis(1))
axis_Y = tas.set_construct(cf.DomainAxis(10))
axis_X = tas.set_construct(cf.DomainAxis(9))

# Set the field construct data
tas.set_data(cf.Data(numpy.arange(90.).reshape(10, 9)))

# Create and set the cell method constructs
cell_method1 = cf.CellMethod(
          axes=[axis_Y, axis_X],
          method='mean',
          qualifiers={'where': 'land',
                      'interval': [cf.Data(0.1, units='degrees')]})

cell_method2 = cf.CellMethod(axes=axis_T, method='maximum')

tas.set_construct(cell_method1)
tas.set_construct(cell_method2)

# Create and set the field ancillary constructs
field_ancillary = cf.FieldAncillary(
             properties={'standard_name': 'air_temperature standard_error',
                          'units': 'K'},
             data=cf.Data(numpy.arange(90.).reshape(10, 9)))

tas.set_construct(field_ancillary)

# Create and set the dimension coordinate constructs
dimension_coordinate_T = cf.DimensionCoordinate(
                           properties={'standard_name': 'time',
                                       'units': 'days since 2018-12-01'},
                           data=cf.Data([15.5]),
                           bounds=cf.Bounds(data=cf.Data([[0., 31]])))

dimension_coordinate_Z = cf.DimensionCoordinate(
        properties={'computed_standard_name': 'altitude',
                    'standard_name': 'atmosphere_hybrid_height_coordinate'},
        data = cf.Data([1.5]),
        bounds=cf.Bounds(data=cf.Data([[1.0, 2.0]])))

dimension_coordinate_Y = cf.DimensionCoordinate(
        properties={'standard_name': 'grid_latitude',
                    'units': 'degrees'},
        data=cf.Data(numpy.arange(10.)),
        bounds=cf.Bounds(data=cf.Data(numpy.arange(20).reshape(10, 2))))

dimension_coordinate_X = cf.DimensionCoordinate(
        properties={'standard_name': 'grid_longitude',
                    'units': 'degrees'},
    data=cf.Data(numpy.arange(9.)),
    bounds=cf.Bounds(data=cf.Data(numpy.arange(18).reshape(9, 2))))

dim_T = tas.set_construct(dimension_coordinate_T, axes=axis_T)
dim_Z = tas.set_construct(dimension_coordinate_Z, axes=axis_Z)
dim_Y = tas.set_construct(dimension_coordinate_Y)
dim_X = tas.set_construct(dimension_coordinate_X)

# Create and set the auxiliary coordinate constructs
auxiliary_coordinate_lat = cf.AuxiliaryCoordinate(
                      properties={'standard_name': 'latitude',
                                  'units': 'degrees_north'},
                      data=cf.Data(numpy.arange(90.).reshape(10, 9)))

auxiliary_coordinate_lon = cf.AuxiliaryCoordinate(
                  properties={'standard_name': 'longitude',
                              'units': 'degrees_east'},
                  data=cf.Data(numpy.arange(90.).reshape(9, 10)))

array = numpy.ma.array(list('abcdefghij'))
array[0] = numpy.ma.masked
auxiliary_coordinate_name = cf.AuxiliaryCoordinate(
                       properties={'long_name': 'Grid latitude name'},
                       data=cf.Data(array))

aux_LAT  = tas.set_construct(auxiliary_coordinate_lat)
aux_LON  = tas.set_construct(auxiliary_coordinate_lon)
aux_NAME = tas.set_construct(auxiliary_coordinate_name)

# Create and set domain ancillary constructs
domain_ancillary_a = cf.DomainAncillary(
                   properties={'units': 'm'},
                   data=cf.Data([10.]),
                   bounds=cf.Bounds(data=cf.Data([[5., 15.]])))

domain_ancillary_b = cf.DomainAncillary(
                       properties={'units': '1'},
                       data=cf.Data([20.]),
                       bounds=cf.Bounds(data=cf.Data([[14, 26.]])))

domain_ancillary_orog = cf.DomainAncillary(
                          properties={'standard_name': 'surface_altitude',
                                      'units': 'm'},
                          data=cf.Data(numpy.arange(90.).reshape(10, 9)))

domain_anc_A    = tas.set_construct(domain_ancillary_a, axes=axis_Z)
domain_anc_B    = tas.set_construct(domain_ancillary_b, axes=axis_Z)
domain_anc_OROG = tas.set_construct(domain_ancillary_orog)

# Create the datum for the coordinate reference constructs
datum = cf.Datum(parameters={'earth_radius': 6371007.})

# Create the coordinate conversion for the horizontal coordinate
# reference construct
coordinate_conversion_h = cf.CoordinateConversion(
              parameters={'grid_mapping_name': 'rotated_latitude_longitude',
                          'grid_north_pole_latitude': 38.0,
                          'grid_north_pole_longitude': 190.0})

# Create the coordinate conversion for the vertical coordinate
# reference construct
coordinate_conversion_v = cf.CoordinateConversion(
         parameters={'standard_name': 'atmosphere_hybrid_height_coordinate',
                     'computed_standard_name': 'altitude'},
         domain_ancillaries={'a': domain_anc_A,
                             'b': domain_anc_B,
                             'orog': domain_anc_OROG})

# Create the vertical coordinate reference construct
horizontal_crs = cf.CoordinateReference(
                   datum=datum,
                   coordinate_conversion=coordinate_conversion_h,
                   coordinates=[dim_X,
                                dim_Y,
                                aux_LAT,
                                aux_LON])

# Create the vertical coordinate reference construct
vertical_crs = cf.CoordinateReference(
                 datum=datum,
                 coordinate_conversion=coordinate_conversion_v,
                 coordinates=[dim_Z])

# Set the coordinate reference constructs
tas.set_construct(horizontal_crs)
tas.set_construct(vertical_crs)

# Create and set the cell measure constructs
cell_measure = cf.CellMeasure(measure='area',
                 properties={'units': 'km2'},
                 data=cf.Data(numpy.arange(90.).reshape(9, 10)))

tas.set_construct(cell_measure)

The new field construct may now be inspected:

Inspect the new field construct.

>>> print(tas)
Field: air_temperature
----------------------
Data            : air_temperature(grid_latitude(10), grid_longitude(9)) K
Cell methods    : grid_latitude(10): grid_longitude(9): mean where land (interval: 0.1 degrees) time(1): maximum
Field ancils    : air_temperature standard_error(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 89.0]] K
Dimension coords: time(1) = [2018-12-16 12:00:00]
                : atmosphere_hybrid_height_coordinate(1) = [1.5]
                : grid_latitude(10) = [0.0, ..., 9.0] degrees
                : grid_longitude(9) = [0.0, ..., 8.0] degrees
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 89.0]] degrees_north
                : longitude(grid_longitude(9), grid_latitude(10)) = [[0.0, ..., 89.0]] degrees_east
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., j]
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[0.0, ..., 89.0]] km2
Coord references: atmosphere_hybrid_height_coordinate
                : rotated_latitude_longitude
Domain ancils   : domainancillary0(atmosphere_hybrid_height_coordinate(1)) = [10.0] m
                : domainancillary1(atmosphere_hybrid_height_coordinate(1)) = [20.0] 1
                : surface_altitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 89.0]] m

Command modification

It is sometimes convenient to produce the commands that would create an already existing field construct, and then modify them to create the desired field constuct. The commands are produced by the creation_commands method of the existing field construct.

Produce the commands that would create an existing field construct.

>>> q, t = cf.read('file.nc')
>>> print(q.creation_commands())
f = cf.Field()

f.set_properties({'Conventions': 'CF-1.7', 'project': 'research', 'standard_name': 'specific_humidity', 'units': '1'})
f.nc_set_variable('q')
f.nc_set_global_attributes({'Conventions': None, 'project': None})

# domain_axis
c = cf.DomainAxis(size=5)
c.nc_set_dimension('lat')
f.set_construct(c, key='domainaxis0')

# domain_axis
c = cf.DomainAxis(size=8)
c.nc_set_dimension('lon')
f.set_construct(c, key='domainaxis1')

# domain_axis
c = cf.DomainAxis(size=1)
f.set_construct(c, key='domainaxis2')

# field data
data = cf.Data([[0.007, 0.034, 0.003, 0.014, 0.018, 0.037, 0.024, 0.029], [0.023, 0.036, 0.045, 0.062, 0.046, 0.073, 0.006, 0.066], [0.11, 0.131, 0.124, 0.146, 0.087, 0.103, 0.057, 0.011], [0.029, 0.059, 0.039, 0.07, 0.058, 0.072, 0.009, 0.017], [0.006, 0.036, 0.019, 0.035, 0.018, 0.037, 0.034, 0.013]], units='1', dtype='f8')
f.set_data(data, axes=('domainaxis0', 'domainaxis1'))

# dimension_coordinate
c = cf.DimensionCoordinate()
c.set_properties({'units': 'degrees_north', 'standard_name': 'latitude'})
c.nc_set_variable('lat')
data = cf.Data([-75.0, -45.0, 0.0, 45.0, 75.0], units='degrees_north', dtype='f8')
c.set_data(data)
b = cf.Bounds()
b.set_properties({'units': 'degrees_north'})
b.nc_set_variable('lat_bnds')
data = cf.Data([[-90.0, -60.0], [-60.0, -30.0], [-30.0, 30.0], [30.0, 60.0], [60.0, 90.0]], units='degrees_north', dtype='f8')
b.set_data(data)
c.set_bounds(b)
f.set_construct(c, axes=('domainaxis0',), key='dimensioncoordinate0', copy=False)

# dimension_coordinate
c = cf.DimensionCoordinate()
c.set_properties({'units': 'degrees_east', 'standard_name': 'longitude'})
c.nc_set_variable('lon')
data = cf.Data([22.5, 67.5, 112.5, 157.5, 202.5, 247.5, 292.5, 337.5], units='degrees_east', dtype='f8')
c.set_data(data)
b = cf.Bounds()
b.set_properties({'units': 'degrees_east'})
b.nc_set_variable('lon_bnds')
data = cf.Data([[0.0, 45.0], [45.0, 90.0], [90.0, 135.0], [135.0, 180.0], [180.0, 225.0], [225.0, 270.0], [270.0, 315.0], [315.0, 360.0]], units='degrees_east', dtype='f8')
b.set_data(data)
c.set_bounds(b)
f.set_construct(c, axes=('domainaxis1',), key='dimensioncoordinate1', copy=False)

# dimension_coordinate
c = cf.DimensionCoordinate()
c.set_properties({'units': 'days since 2018-12-01', 'standard_name': 'time'})
c.nc_set_variable('time')
data = cf.Data([31.0], units='days since 2018-12-01', dtype='f8')
c.set_data(data)
f.set_construct(c, axes=('domainaxis2',), key='dimensioncoordinate2', copy=False)

# cell_method
c = cf.CellMethod()
c.method = 'mean'
c.axes = ('area',)
f.set_construct(c)

Some example fields are always available from the cf.example_field function.

Creating data from an array on disk

All the of above examples use arrays in memory to construct the data instances for the field and metadata constructs. It is, however, possible to create data from arrays that reside on disk. The cf.read function creates data in this manner. A pointer to an array in a netCDF file can be stored in a cf.NetCDFArray instance, which is is used to initialize a cf.Data instance.

Define a variable from a dataset with the netCDF package and use it to create a NetCDFArray instance with which to initialize a Data instance.

>>> import netCDF4
>>> nc = netCDF4.Dataset('file.nc', 'r')
>>> v = nc.variables['ta']
>>> netcdf_array = cf.NetCDFArray(filename='file.nc', ncvar='ta',
...                                 dtype=v.dtype, ndim=v.ndim,
...                                 shape=v.shape, size=v.size)
>>> data_disk = cf.Data(netcdf_array)

Read the netCDF variable’s data into memory and initialise another Data instance with it. Compare the values of the two data instances.

>>> numpy_array = v[...]
>>> data_memory = cf.Data(numpy_array)
>>> data_disk.equals(data_memory)
True

Note that data type, number of dimensions, dimension sizes and number of elements of the array on disk that are used to initialize the cf.NetCDFArray instance are those expected by the CF data model, which may be different to those of the netCDF variable in the file (although they are the same in the above example). For example, a netCDF character array of shape (12, 9) is viewed in cf as a one-dimensional string array of shape (12,).

Creation by conversion

An independent field construct may be created from an existing metadata construct using convert method of the field construct, which identifies a unique metadata construct and returns a new field construct based on its properties and data. The new field construct always has domain axis constructs corresponding to the data, and (by default) any other metadata constructs that further define its domain.

Create an independent field construct from the “surface altitude” metadata construct.

>>> key = tas.construct_key('surface_altitude')
>>> orog = tas.convert(key)
>>> print(orog)
Field: surface_altitude
-----------------------
Data            : surface_altitude(grid_latitude(10), grid_longitude(9)) m
Dimension coords: grid_latitude(10) = [0.0, ..., 9.0] degrees
                : grid_longitude(9) = [0.0, ..., 8.0] degrees
Auxiliary coords: latitude(grid_latitude(10), grid_longitude(9)) = [[0.0, ..., 89.0]] degrees_north
                : longitude(grid_longitude(9), grid_latitude(10)) = [[0.0, ..., 89.0]] degrees_east
                : long_name=Grid latitude name(grid_latitude(10)) = [--, ..., j]
Cell measures   : measure:area(grid_longitude(9), grid_latitude(10)) = [[0.0, ..., 89.0]] km2
Coord references: rotated_latitude_longitude

The convert method has an option to only include domain axis constructs in the new field construct, with no other metadata constructs.

Create an independent field construct from the “surface altitude” metadata construct, but without a complete domain.

>>> orog1 = tas.convert(key, full_domain=False)
>>> print(orog1)
Field: surface_altitude
-----------------------
Data            : surface_altitude(key%domainaxis2(10), key%domainaxis3(9)) m

Creation by reading

The cf.read function reads a netCDF dataset and returns the contents as a list of zero or more field constructs, each one corresponding to a unique CF-netCDF data variable in the dataset. For example, the field construct tas that was created manually can be written to a netCDF dataset and then read back into memory:

Write the field construct that was created manually to disk, and then read it back into a new field construct.

>>> cf.write(tas, 'tas.nc')
>>> f = cf.read('tas.nc')
>>> f
[<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>]

The cf.read function also allows field constructs to be derived directly from the netCDF variables that correspond to particular types metadata constructs. In this case, the new field constructs will have a domain limited to that which can be inferred from the corresponding netCDF variable, but without the connections that are defined by the parent netCDF data variable. This will often result in a new field construct that has fewer metadata constructs than one created with the convert method.

Read the file, treating formula terms netCDF variables (which map to domain ancillary constructs) as additional CF-netCDF data variables.

>>> fields = cf.read('tas.nc', extra='domain_ancillary')
>>> fields
[<CF Field: ncvar%a(atmosphere_hybrid_height_coordinate(1)) m>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>,
 <CF Field: ncvar%b(atmosphere_hybrid_height_coordinate(1)) 1>,
 <CF Field: surface_altitude(grid_latitude(10), grid_longitude(9)) m>]
>>> orog_from_file = fields[3]
>>> print(orog_from_file)
Field: surface_altitude (ncvar%surface_altitude)
------------------------------------------------
Data            : surface_altitude(grid_latitude(10), grid_longitude(9)) m
Dimension coords: grid_latitude(10) = [0.0, ..., 9.0] degrees
                : grid_longitude(9) = [0.0, ..., 8.0] degrees

Comparing the field constructs orog_from_file (created with cf.read) and orog (created with the convert method of the tas field construct), the former lacks the auxiliary coordinate, cell measure and coordinate reference constructs of the latter. This is because the surface altitude netCDF variable in tas.nc does not have the “coordinates”, “cell_measures” nor “grid_mapping” netCDF attributes that would link it to auxiliary coordinate, cell measure and grid mapping netCDF variables.

Creation with cfa

The cfa command line tool may be used to inspect datasets on disk and also to create new datasets from them. Aggregation may be carried out within files, or within and between files, or not used; and external variables may be incorporated.

Use cfa to create new, single dataset that combines the field constructs from two files.

$ cfa file.nc
CF Field: specific_humidity(latitude(5), longitude(8)) 1
CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
$ cfa air_temperature.nc
CF Field: air_temperature(time(2), latitude(73), longitude(96)) K
$ cfa -o new_dataset.nc file.nc air_temperature.nc
$ cfa  new_dataset.nc
CF Field: specific_humidity(latitude(5), longitude(8)) 1
CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K
CF Field: air_temperature(time(2), latitude(73), longitude(96)) K

---

Copying

A field construct may be copied with its copy method. This produces a “deep copy”, i.e. the new field construct is completely independent of the original field.

Copy a field construct and change elements of the copy, showing that the original field construct has not been altered.

>>> u = t.copy()
>>> u.data[0, 0, 0] = -1e30
>>> u.data[0, 0, 0]
<CF Data(1, 1, 1): [[[-1e+30]]] K>
>>> t.data[0, 0, 0]
<CF Data(1, 1, 1): [[[-1.0]]] K>
>>> u.del_construct('grid_latitude')
<CF DimensionCoordinate: grid_latitude(10) degrees>
>>> u.constructs('grid_latitude')
{}
>>> t.constructs('grid_latitude')
{'dimensioncoordinate1': <CF DimensionCoordinate: grid_latitude(10) degrees>}

Equivalently, the copy.deepcopy function may be used:

Copy a field construct with the built-in copy module.

>>> import copy
>>> u = copy.deepcopy(t)

Metadata constructs may be copied individually in the same manner:

Copy a metadata construct.

>>> orog = t.constructs('surface_altitude').value().copy()

Arrays within cf.Data instances are copied with a copy-on-write technique. This means that a copy takes up very little memory, even when the original constructs contain very large data arrays, and the copy operation is fast.

Field list copying

A field list also has a copy method that creates a new field list containing copies all of the field construct elements.

---

Equality

Whether or not two field constructs are the same is tested with either field construct’s equals method.

A field construct is always equal to itself, a copy of itself and a complete subspace of itself. The “verbose” keyword will give some (but not necessarily all) of the reasons why two field constructs are not the same.

>>> t.equals(t)
True
>>> t.equals(t.copy())
True
>>> t.equals(t[...])
True
>>> t.equals(q)
False
>>> t.equals(q, verbose=True)
Field: Different Units: <Units: K> != <Units: 1>
False

Equality is strict by default. This means that for two field constructs to be considered equal they must have corresponding metadata constructs and for each pair of constructs:

• the descriptive properties must be the same (with the exception of the field construct’s “Conventions” property, which is never checked), and vector-valued properties must have same the size and be element-wise equal, and

• if there are data arrays then they must have same shape, data type and be element-wise equal.

Two real numbers \(x\) and \(y\) are considered equal if \(|x - y| \le a_{tol} + r_{tol}|y|\), where \(a_{tol}\) (the tolerance on absolute differences) and \(r_{tol}\) (the tolerance on relative differences) are positive, typically very small numbers. By default both are set to the system epsilon (the difference between 1 and the least value greater than 1 that is representable as a float). Their values may be inspected and changed with the cf.ATOL and cf.RTOL functions:

The ATOL and RTOL functions allow the numerical equality tolerances to be inspected and changed.

>>> cf.ATOL()
2.220446049250313e-16
>>> cf.RTOL()
2.220446049250313e-16
>>> original = cf.RTOL(0.00001)
>>> cf.RTOL()
1e-05
>>> cf.RTOL(original)
1e-05
>>> cf.RTOL()
2.220446049250313e-16

Note that the above equation is not symmetric in \(x\) and \(y\), so that for two fields f1 and f2, f1.equals(f2) may be different from f2.equals(f1) in some rare cases.

NetCDF elements, such as netCDF variable and dimension names, do not constitute part of the CF data model and so are not checked on any construct.

The equals method has optional parameters for modifying the criteria for considering two fields to be equal:

• named properties may be omitted from the comparison,

• fill value and missing data value properties may be ignored,

• the data type of data arrays may be ignored, and

• the tolerances on absolute and relative differences for numerical comparisons may be temporarily changed, without changing the default settings.

Metadata constructs may also be tested for equality:

Metadata constructs also have an equals method, that behaves in a similar manner.

>>> orog = t.constructs('surface_altitude').value()
>>> orog.equals(orog.copy())
True

Field list equality

A field list also has an equals method that compares two field lists. It returns True if and only if field constructs at the same index are equal. This method also has an unordered parameter that, when True, treats the two field lists as unordered collections of field constructs, i.e. in this case True is returned if and only if field constructs are pair-wise equal, irrespective of their positions in the list.

---

NetCDF interface

The logical CF data model is independent of netCDF, but the CF conventions are designed to enable the processing and sharing of datasets stored in netCDF files. Therefore, the cf package includes methods for recording and editing netCDF elements that are not part of the CF model, but are nonetheless often required to interpret and create CF-netCDF datasets. See the section on philosophy for a further discussion.

When a netCDF dataset is read, netCDF elements (such as dimension and variable names, and some attribute values) that do not have a place in the CF data model are, nevertheless, stored within the appropriate cf constructs. This allows them to be used when writing field constructs to a new netCDF dataset, and also makes them accessible as filters to a cf.Constructs instance:

Retrieve metadata constructs based on their netCDF names.

>>> print(t.constructs.filter_by_ncvar('b'))
Constructs:
{'domainancillary1': <CF DomainAncillary: ncvar%b(1) >}
>>> t.constructs('ncvar%x').value()
<CF DimensionCoordinate: grid_longitude(9) degrees>
>>> t.constructs('ncdim%x')
<CF Constructs: domain_axis(1)>

Each construct has methods to access the netCDF elements which it requires. For example, the field construct has the following methods:

Method	Description
nc_get_variable	Return the netCDF variable name
nc_set_variable	Set the netCDF variable name
nc_del_variable	Remove the netCDF variable name
nc_has_variable	Whether the netCDF variable name has been set
nc_global_attributes	Return the selection of properties to be written as netCDF global attributes
nc_set_global_attribute	Set a property to be written as a netCDF global attribute
nc_set_global_attributes	Set properties to be written as netCDF global attributes
nc_clear_global_attributes	Clear the selection of properties to be written as netCDF global attributes

Access netCDF elements associated with the field and metadata constructs.

>>> q.nc_get_variable()
'q'
>>> q.nc_global_attributes()
{'Conventions': None, 'project': None}
>>> q.nc_set_variable('humidity')
>>> q.nc_get_variable()
'humidity'
>>> q.constructs('latitude').value().nc_get_variable()
'lat'

The complete collection of netCDF interface methods is:

Method	Classes	NetCDF element
nc_del_variable	cf.Field, cf.DimensionCoordinate, cf.AuxiliaryCoordinate, CellMeasure, cf.DomainAncillary, cf.FieldAncillary, cf.CoordinateReference, cf.Bounds, cf.Datum, cf.Count, cf.Index, cf.List	Variable name
nc_get_variable	cf.Field, cf.DimensionCoordinate, cf.AuxiliaryCoordinate, CellMeasure, cf.DomainAncillary, cf.FieldAncillary, cf.CoordinateReference, cf.Bounds, cf.Datum, cf.Count, cf.Index, cf.List	Variable name
nc_has_variable	cf.Field, cf.DimensionCoordinate, cf.AuxiliaryCoordinate, CellMeasure, cf.DomainAncillary, cf.FieldAncillary, cf.CoordinateReference, cf.Bounds, cf.Datum, cf.Count, cf.Index, cf.List	Variable name
nc_set_variable	cf.Field, cf.DimensionCoordinate, cf.AuxiliaryCoordinate, CellMeasure, cf.DomainAncillary, cf.FieldAncillary, cf.CoordinateReference, cf.Bounds, cf.Datum, cf.Count, cf.Index, cf.List	Variable name
nc_del_dimension	cf.DomainAxis, cf.Count, cf.Index	Dimension name
nc_get_dimension	cf.DomainAxis, cf.Count, cf.Index	Dimension name
nc_has_dimension	cf.DomainAxis, cf.Count, cf.Index	Dimension name
nc_set_dimension	cf.DomainAxis, cf.Count, cf.Index	Dimension name
nc_is_unlimited	cf.DomainAxis	Unlimited dimension
nc_set_unlimited	cf.DomainAxis	Unlimited dimension
nc_global_attributes	cf.Field	Global attributes
nc_set_global_attribute	cf.Field	Global attributes
nc_set_global_attributes	cf.Field	Global attributes
nc_clear_global_attributes	cf.Field	Global attributes
nc_get_external	cf.CellMeasure	External variable status
nc_set_external	cf.CellMeasure	External variable status
nc_del_sample_dimension	cf.Count, cf.Index	Sample dimension name
nc_get_sample_dimension	cf.Count, cf.Index	Sample dimension name
nc_has_sample_dimension	cf.Count, cf.Index	Sample dimension name
nc_set_sample_dimension	cf.Count, cf.Index	Sample dimension name

---

Writing to a netCDF dataset

The cf.write function writes a field construct, or a sequence of field constructs, to a new netCDF file on disk:

Write a field construct to a netCDF dataset on disk.

>>> print(q)
Field: specific_humidity (ncvar%humidity)
-----------------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> cf.write(q, 'q_file.nc')

The new dataset is structured as follows:

Inspect the new dataset with the ncdump command line tool.

$ ncdump -h q_file.nc
netcdf q_file {
dimensions:
     lat = 5 ;
     bounds2 = 2 ;
     lon = 8 ;
variables:
     double lat_bnds(lat, bounds2) ;
     double lat(lat) ;
             lat:units = "degrees_north" ;
             lat:standard_name = "latitude" ;
             lat:bounds = "lat_bnds" ;
     double lon_bnds(lon, bounds2) ;
     double lon(lon) ;
             lon:units = "degrees_east" ;
             lon:standard_name = "longitude" ;
             lon:bounds = "lon_bnds" ;
     double time ;
             time:units = "days since 2018-12-01" ;
             time:standard_name = "time" ;
     double humidity(lat, lon) ;
             humidity:standard_name = "specific_humidity" ;
             humidity:cell_methods = "area: mean" ;
             humidity:units = "1" ;
             humidity:coordinates = "time" ;

// global attributes:
             :Conventions = "CF-1.7" ;
             :project = "research" ;
}

Note that netCDF is the only available output file format.

A sequence of field constructs is written in exactly the same way:

Write multiple field constructs to a netCDF dataset on disk.

>>> x
[<CF Field: specific_humidity(latitude(5), longitude(8)) 1>,
 <CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>]
>>> cf.write(x, 'new_file.nc')

By default the output file will be for CF-1.8.

The cf.write function has optional parameters to

• set the output netCDF format (all netCDF3 and netCDF4 formats are possible);

• specify which field construct properties should become netCDF data variable attributes and which should become netCDF global attributes;

• set extra netCDF global attributes;

• create external variables in an external file;

• specify the version of the CF conventions (from CF-1.6 up to CF-1.8), and of any other conventions that the file adheres to;

• change the data type of output data arrays;

• apply netCDF compression and packing; and

• set the endian-ness of the output data.

Output netCDF variable and dimension names read from a netCDF dataset are stored in the resulting field constructs, and may also be set manually with the nc_set_variable, nc_set_dimension and nc_set_sample_dimension methods. If a name has not been set then one will be generated internally (usually based on the standard name if it exists).

It is possible to create netCDF unlimited dimensions using the nc_set_unlimited method of the domain axis construct.

A field construct is not transformed through being written to a file on disk and subsequently read back from that file.

Read a file that has been created by writing a field construct, and compare the result with the original field construct in memory.

>>> f = cf.read('q_file.nc')[0]
>>> q.equals(f)
True

Global attributes

The field construct properties that correspond to the standardised description-of-file-contents attributes are automatically written as netCDF global attributes. Other attributes may also be written as netCDF global attributes if they have been identified as such with the global_attributes keyword, or via the nc_set_global_attribute or nc_set_global_attributes methods of the field constructs. In either case, the creation of a netCDF global attribute depends on the corresponding property values being identical across all of the field constructs being written to the file. If they are all equal then the property will be written as a netCDF global attribute and not as an attribute of any netCDF data variable; if any differ then the property is written only to each netCDF data variable.

Request that the “model” property is written as a netCDF global attribute, using the “global_attributes” keyword.

>>> f.set_property('model', 'model_A')
>>> cf.write(f, 'f_file.nc', global_attributes='model')

Request that the “model” property is written as a netCDF global attribute, using the “nc_set_global_attribute” method.

>>> f.nc_global_attributes()
{'Conventions': None, 'project': None}
>>> f.nc_set_global_attribute('model')
>>> f.nc_global_attributes()
{'Conventions': None, 'project': None, 'model': None}
>>> cf.write(f, 'f_file.nc')

It is possible to create both a netCDF global attribute and a netCDF data variable attribute with the same name, but with different values. This may be done by assigning the global value to the property name with the nc_set_global_attribute or nc_set_global_attributes method, or by via the file_descriptors keyword. For the former technique, any inconsistencies arising from multiple field constructs being written to the same file will be resolved by omitting the netCDF global attribute from the file.

Request that the “information” property is written as netCDF global and data variable attributes, with different values, using the “nc_set_global_attribute” method.

>>> f.set_property('information', 'variable information')
>>> f.properties()
{'Conventions': 'CF-1.7',
 'information': 'variable information',
 'project': 'research',
 'standard_name': 'specific_humidity',
 'units': '1'}
>>> f.nc_set_global_attribute('information', 'global information')
>>> f.nc_global_attributes()
{'Conventions': None,
'information': 'global information',
 'model': None,
 'project': None}
>>> cf.write(f, 'f_file.nc')

NetCDF global attributes defined with the file_descriptors keyword of the cf.write function will always be written as requested, independently of the netCDF data variable attributes, and superseding any global attributes that may have been defined with the global_attributes keyword, or set on the individual field constructs.

Insist that the “history” property is written as netCDF a global attribute, with the “file_descriptors” keyword.

>>> cf.write(f, 'f_file.nc', file_descriptors={'history': 'created in 2019'})
>>> f_file = cf.read('f_file.nc')[0]
>>> f_file.nc_global_attributes()
>>> f_file.properties()
{'Conventions': 'CF-1.7',
 'history': 'created in 2019',
 'information': 'variable information',
 'model': 'model_A',
 'project': 'research',
 'standard_name': 'specific_humidity',
 'units': '1'}
>>> f_file.nc_global_attributes()
{'Conventions': None,
 'history': None,
 'information': 'global information',
 'project': None}

Conventions

The “Conventions” netCDF global attribute containing the version of the CF conventions is always automatically created. If the version of the CF conventions has been set as a field property, or with the Conventions keyword of the cf.write function, then it is ignored. However, other conventions that may apply can be set with either technique.

Two ways to add additional conventions to the “Conventions” netCDF global attribute.

>>> f_file.set_property('Conventions', 'UGRID1.0')
>>> cf.write(f, 'f_file.nc', Conventions='UGRID1.0')

Scalar coordinate variables

A CF-netCDF scalar (i.e. zero-dimensional) coordinate variable is created from a size one dimension coordinate construct that spans a domain axis construct which is not spanned by the field construct’s data, nor the data of any other metadata construct. This occurs for the field construct q, for which the “time” dimension coordinate construct was to the file q_file.nc as a scalar coordinate variable.

To change this so that the “time” dimension coordinate construct is written as a CF-netCDF size one coordinate variable, the field construct’s data must be expanded to span the corresponding size one domain axis construct, by using the insert_dimension method of the field construct.

Write the “time” dimension coordinate construct to a (non-scalar) CF-netCDF coordinate variable by inserting the corresponding dimension into the field construct’s data.

>>> print(q)
Field: specific_humidity (ncvar%humidity)
-----------------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
<CF Field: specific_humidity(latitude(5), longitude(8)) 1>
>>> key = q.construct_key('time')
>>> axes = q.get_data_axes(key)
>>> axes
('domainaxis2',)
>>> q2 = q.insert_dimension(axis=axes[0])
>>> q2
<CF Field: specific_humidity(time(1), latitude(5), longitude(8)) 1>
>>> cf.write(q2, 'q2_file.nc')

The new dataset is structured as follows (note, relative to file q_file.nc, the existence of the “time” dimension and the lack of a “coordinates” attribute on the, now three-dimensional, data variable):

Inspect the new dataset with the ncdump command line tool.

$ ncdump -h q2_file.nc
netcdf q2_file {
dimensions:
     lat = 5 ;
     bounds2 = 2 ;
     lon = 8 ;
     time = 1 ;
variables:
     double lat_bnds(lat, bounds2) ;
     double lat(lat) ;
             lat:units = "degrees_north" ;
             lat:standard_name = "latitude" ;
             lat:bounds = "lat_bnds" ;
     double lon_bnds(lon, bounds2) ;
     double lon(lon) ;
             lon:units = "degrees_east" ;
             lon:standard_name = "longitude" ;
             lon:bounds = "lon_bnds" ;
     double time(time) ;
             time:units = "days since 2018-12-01" ;
             time:standard_name = "time" ;
     double humidity(time, lat, lon) ;
             humidity:units = "1" ;
             humidity:standard_name = "specific_humidity" ;
             humidity:cell_methods = "area: mean" ;

// global attributes:
             :Conventions = "CF-1.7" ;
             :project = "research" ;
}

Strings

String-valued data may be written to netCDF files either as netCDF character arrays with a trailing dimension large enough to contain the longest value, or as netCDF4 string arrays. The former is allowed for all formats of netCDF3 and netCDF4 format files; but string arrays may only be written to netCDF4 format files (note that string arrays can not be written to netCDF4 classic format files).

By default, netCDF string arrays will be created whenever possible, and in all other cases netCDF character arrays will be used. Alternatively, netCDF character arrays can be used in all cases by setting the string keyword of the cf.write function.

---

Hierarchical groups

Hierarchical groups provide a powerful mechanism to structure variables within datasets. A future release of cf will include support for netCDF4 files containing data organised in hierarchical groups, but this is not available in version 3.2.0 (even though it is allowed in CF-1.8).

---

External variables

External variables are those in a netCDF file that are referred to, but which are not present in it. Instead, such variables are stored in other netCDF files known as “external files”. External variables may, however, be incorporated into the field constructs of the dataset, as if they had actually been stored in the same file, simply by providing the external file names to the cf.read function.

This is illustrated with the files parent.nc (found in the sample datasets):

Inspect the parent dataset with the ncdump command line tool.

$ ncdump -h parent.nc
netcdf parent {
dimensions:
     latitude = 10 ;
     longitude = 9 ;
variables:
     double latitude(latitude) ;
             latitude:units = "degrees_north" ;
             latitude:standard_name = "latitude" ;
     double longitude(longitude) ;
             longitude:units = "degrees_east" ;
             longitude:standard_name = "longitude" ;
     double eastward_wind(latitude, longitude) ;
             eastward_wind:units = "m s-1" ;
             eastward_wind:standard_name = "eastward_wind" ;
             eastward_wind:cell_measures = "area: areacella" ;

// global attributes:
             :Conventions = "CF-1.7" ;
             :external_variables = "areacella" ;
}

and external.nc (found in the sample datasets):

Inspect the external dataset with the ncdump command line tool.

$ ncdump -h external.nc
netcdf external {
dimensions:
     latitude = 10 ;
     longitude = 9 ;
variables:
     double areacella(longitude, latitude) ;
             areacella:units = "m2" ;
             areacella:standard_name = "cell_area" ;

// global attributes:
             :Conventions = "CF-1.7" ;
}

The dataset in parent.nc may be read without specifying the external file external.nc. In this case a cell measure construct is still created, but one without any metadata or data:

Read the parent dataset without specifying the location of any external datasets.

>>> u = cf.read('parent.nc')[0]
>>> print(u)
Field: eastward_wind (ncvar%eastward_wind)
------------------------------------------
Data            : eastward_wind(latitude(10), longitude(9)) m s-1
Dimension coords: latitude(10) = [0.0, ..., 9.0] degrees
                : longitude(9) = [0.0, ..., 8.0] degrees
Cell measures   : measure:area (external variable: ncvar%areacella)

>>> area = u.constructs('measure:area').value()
>>> area
<CF CellMeasure: measure:area >
>>> area.nc_get_external()
True
>>> area.nc_get_variable()
'areacella'
>>> area.properties()
{}
>>> area.has_data()
False

If this field construct were to be written to disk using cf.write, then the output file would be identical to the original parent.nc file, i.e. the netCDF variable name of the cell measure construct (“areacella”) would be listed by the “external_variables” global attribute.

However, the dataset may also be read with the external file. In this case a cell measure construct is created with all of the metadata and data from the external file, as if the netCDF cell measure variable had been present in the parent dataset:

Read the parent dataset whilst providing the external dataset containing the external variables.

>>> g = cf.read('parent.nc', external='external.nc')[0]
>>> print(g)
Field: eastward_wind (ncvar%eastward_wind)
------------------------------------------
Data            : eastward_wind(latitude(10), longitude(9)) m s-1
Dimension coords: latitude(10) = [0.0, ..., 9.0] degrees
                : longitude(9) = [0.0, ..., 8.0] degrees
Cell measures   : measure:area(longitude(9), latitude(10)) = [[100000.5, ..., 100089.5]] m2
>>> area = g.construct('measure:area')
>>> area
<CF CellMeasure: measure:area(9, 10) m2>
>>> area.nc_get_external()
False
>>> area.nc_get_variable()
'areacella'
>>> area.properties()
{'standard_name': 'cell_area', 'units': 'm2'}
>>> area.data
<CF Data(9, 10): [[100000.5, ..., 100089.5]] m2>

If this field construct were to be written to disk using cf.write then by default the cell measure construct, with all of its metadata and data, would be written to the named output file, along with all of the other constructs. There would be no “external_variables” global attribute.

To create a reference to an external variable in an output netCDF file, set the status of the cell measure construct to “external” with its nc_set_external method.

Flag the cell measure as external and write the field construct to a new file.

>>> area.nc_set_external(True)
>>> cf.write(g, 'new_parent.nc')

To create a reference to an external variable in the an output netCDF file and simultaneously create an external file containing the variable, set the status of the cell measure construct to “external” and provide an external file name to the cf.write function:

Write the field construct to a new file and the cell measure construct to an external file.

>>> cf.write(g, 'new_parent.nc', external='new_external.nc')

External files with cfa

One or more external files may also be included with the cfa command line tool.

Use cfa to describe the parent file without resolving the external variable reference.

$ cfa parent.nc
Field: eastward_wind (ncvar%eastward_wind)
------------------------------------------
Data            : eastward_wind(latitude(10), longitude(9)) m s-1
Dimension coords: latitude(10) = [0.0, ..., 9.0] degrees_north
                : longitude(9) = [0.0, ..., 8.0] degrees_east
Cell measures   : measure:area (external variable: ncvar%areacella)

Providing an external file with the “-e” option allows the reference to be resolved.

$ cfa -e external.nc parent.nc
Field: eastward_wind (ncvar%eastward_wind)
------------------------------------------
Data            : eastward_wind(latitude(10), longitude(9)) m s-1
Dimension coords: latitude(10) = [0.0, ..., 9.0] degrees_north
                : longitude(9) = [0.0, ..., 8.0] degrees_east
Cell measures   : measure:area(longitude(9), latitude(10)) = [[100000.5, ..., 100089.5]] m2

External variables will be written into new datasets if the -v option is omitted.

---

Aggregation

Aggregation is the combination of field constructs to create a new field construct that occupies a “larger” domain. Using the aggregation rules, field constructs are separated into aggregatable groups and each group is then aggregated to a single field construct. Note that aggregation is possible over multiple dimensions simultaneously.

Aggregation is, by default, applied to field constructs read from datasets with the cf.read function, but may also be applied to field constructs in memory with the cf.aggregate function.

Demonstrate that the aggregation applied by ‘cf.read’ is equivalent to that carried by ‘cf.aggregate’. This is done by splitting a field up into parts, writing those to disk, and then reading those parts and aggregating them.

>>> a = cf.read('air_temperature.nc')[0]
>>> a
<CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>
>>> a_parts = [a[0, : , 0:30], a[0, :, 30:96], a[1, :, 0:30], a[1, :, 30:96]]
>>> a_parts
[<CF Field: air_temperature(time(1), latitude(73), longitude(30)) K>,
 <CF Field: air_temperature(time(1), latitude(73), longitude(66)) K>,
 <CF Field: air_temperature(time(1), latitude(73), longitude(30)) K>,
 <CF Field: air_temperature(time(1), latitude(73), longitude(66)) K>]
>>> for i, f in enumerate(a_parts):
...     cf.write(f, str(i)+'_air_temperature.nc')
...
>>> x = cf.read('[0-3]_air_temperature.nc')
>>> y = cf.read('[0-3]_air_temperature.nc', aggregate=False)
>>> z = cf.aggregate(y)
>>> x
[<CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>]
>>> z
[<CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>]
>>> x.equals(z)
True

The cf.aggregate function has optional parameters to

• Display information about the aggregation process,

• Relax the conditions to the need for standard names and units properties,

• Specify whether or not to allow field constructs with overlapping or non-contiguous cells to be aggregated,

• Define the treatment of properties with different values across the set of aggregated field constructs,

• Create a new aggregated domain axes with coordinate values taken from a named field construct property,

• Restrict aggregation to particular domain axes, and

• Set the tolerance for numerical comparisons.

These parameters are also available to the cf.read function via its aggregate parameter.

Note that when reading PP and UM fields files with cf.read, the relaxed_units option is True by default, because units are not always available to field constructs derived from PP and UM fields files.

Field constructs that are logically similar but arranged differently are also aggregatable.

Show that the aggregation is unchanged when one of the field constructs has a different axis order and different units.

>>> x = cf.aggregate(a_parts)
>>> x
[<CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>]
>>> a_parts[1].transpose(inplace=True)
>>> a_parts[1].units = 'degreesC'
>>> a_parts
[<CF Field: air_temperature(time(1), latitude(73), longitude(30)) K>,
 <CF Field: air_temperature(longitude(66), latitude(73), time(1)) degreesC>,
 <CF Field: air_temperature(time(1), latitude(73), longitude(30)) K>,
 <CF Field: air_temperature(time(1), latitude(73), longitude(66)) K>]
>>> z = cf.aggregate(a_parts)
>>> z
[<CF Field: air_temperature(time(2), latitude(73), longitude(96)) K>]
>>> x.equals(z)
True

---

Compression

The CF conventions have support for saving space by identifying and removing unwanted missing data. Such compression techniques store the data more efficiently and result in no precision loss. The CF data model, however, views compressed arrays in their uncompressed form.

Therefore, the field construct contains domain axis constructs for the compressed dimensions and presents a view of compressed data in its uncompressed form, even though the “underlying array” (i.e. the actual array on disk or in memory that is contained in a cf.Data instance) is compressed. This means that the cf package includes algorithms for uncompressing each type of compressed array.

There are two basic types of compression supported by the CF conventions: ragged arrays (as used by discrete sampling geometries) and compression by gathering, each of which has particular implementation details, but the following access patterns and behaviours apply to both:

• Whether or not the data are compressed is tested with the get_compression_type method of the cf.Data instance.

• The compressed underlying array may be retrieved as a numpy array with the compressed_array attribute of the cf.Data instance.

• Accessing the data via the array attribute returns a numpy array that is uncompressed. The underlying array will also be uncompressed.

• A subspace of a field construct is created with indices of the uncompressed form of the data. The new subspace will no longer be compressed, i.e. its underlying arrays will be uncompressed, but the original data will remain compressed. It follows that all of the data in a field construct may be uncompressed by indexing the field construct with (indices equivalent to) Ellipsis.

• If data elements are modified by assigning to indices of the uncompressed form of the data, then the compressed underlying array is replaced by its uncompressed form.

• An uncompressed field construct can be compressed, prior to being written to a dataset, with its compress method, which also compresses the metadata constructs as required.

• An compressed field construct can be uncompressed with its uncompress method, which also uncompresses the metadata constructs as required.

• If an underlying array is compressed at the time of writing to disk with the cf.write function, then it is written to the file as a compressed array, along with the supplementary netCDF variables and attributes that are required for the encoding. This means that if a dataset using compression is read from disk then it will be written back to disk with the same compression, unless data elements have been modified by assignment.

Examples of all of the above may be found in the sections on discrete sampling geometries and gathering.

Discrete sampling geometries

Discrete sampling geometry (DSG) features may be compressed by combining them using one of three ragged array representations: contiguous, indexed or indexed contiguous.

The count variable that is required to uncompress a contiguous, or indexed contiguous, ragged array is stored in a cf.Count instance and is accessed with the get_count method of the cf.Data instance.

The index variable that is required to uncompress an indexed, or indexed contiguous, ragged array is stored in an cf.Index instance and is accessed with the get_index method of the cf.Data instance.

The contiguous case is is illustrated with the file contiguous.nc (found in the sample datasets):

Inspect the compressed dataset with the ncdump command line tool.

$ ncdump -h contiguous.nc
dimensions:
     station = 4 ;
     obs = 24 ;
     strlen8 = 8 ;
variables:
     int row_size(station) ;
             row_size:long_name = "number of observations for this station" ;
             row_size:sample_dimension = "obs" ;
     double time(obs) ;
             time:units = "days since 1970-01-01 00:00:00" ;
             time:standard_name = "time" ;
     double lat(station) ;
             lat:units = "degrees_north" ;
             lat:standard_name = "latitude" ;
     double lon(station) ;
             lon:units = "degrees_east" ;
             lon:standard_name = "longitude" ;
     double alt(station) ;
             alt:units = "m" ;
             alt:positive = "up" ;
             alt:standard_name = "height" ;
             alt:axis = "Z" ;
     char station_name(station, strlen8) ;
             station_name:long_name = "station name" ;
             station_name:cf_role = "timeseries_id" ;
     double humidity(obs) ;
             humidity:standard_name = "specific_humidity" ;
             humidity:coordinates = "time lat lon alt station_name" ;
             humidity:_FillValue = -999.9 ;

// global attributes:
             :Conventions = "CF-1.7" ;
             :featureType = "timeSeries" ;
}

Reading and inspecting this file shows the data presented in two-dimensional uncompressed form, whilst the underlying array is still in the one-dimension ragged representation described in the file:

Read a field construct from a dataset that has been compressed with contiguous ragged arrays, and inspect its data in uncompressed form.

>>> h = cf.read('contiguous.nc')[0]
>>> print(h)
Field: specific_humidity (ncvar%humidity)
-----------------------------------------
Data            : specific_humidity(ncdim%station(4), ncdim%timeseries(9))
Dimension coords:
Auxiliary coords: time(ncdim%station(4), ncdim%timeseries(9)) = [[1969-12-29 00:00:00, ..., 1970-01-07 00:00:00]]
                : latitude(ncdim%station(4)) = [-9.0, ..., 78.0] degrees_north
                : longitude(ncdim%station(4)) = [-23.0, ..., 178.0] degrees_east
                : height(ncdim%station(4)) = [0.5, ..., 345.0] m
                : cf_role:timeseries_id(ncdim%station(4)) = [station1, ..., station4]
>>> print(h.array)
[[0.12 0.05 0.18   --   --   --   --   --   --]
 [0.05 0.11 0.2  0.15 0.08 0.04 0.06   --   --]
 [0.15 0.19 0.15 0.17 0.07   --   --   --   --]
 [0.11 0.03 0.14 0.16 0.02 0.09 0.1  0.04 0.11]]

Inspect the underlying compressed array and the count variable that defines how to uncompress the data.

>>> h.data.get_compression_type()
'ragged contiguous'
>>> print(h.data.compressed_array)
[0.12 0.05 0.18 0.05 0.11 0.2 0.15 0.08 0.04 0.06 0.15 0.19 0.15 0.17 0.07
 0.11 0.03 0.14 0.16 0.02 0.09 0.1 0.04 0.11]
>>> count_variable = h.data.get_count()
>>> count_variable
<CF Count: long_name=number of observations for this station(4) >
>>> print(count_variable.array)
[3 7 5 9]

The timeseries for the second station is easily selected by indexing the “station” axis of the field construct:

Get the data for the second station.

>>> station2 = h[1]
>>> station2
<CF Field: specific_humidity(cf_role=timeseries_id(1), ncdim%timeseries(9))>
>>> print(station2.array)
[[0.05 0.11 0.2 0.15 0.08 0.04 0.06 -- --]]

The underlying array of original data remains in compressed form until data array elements are modified:

Change an element of the data and show that the underlying array is no longer compressed.

>>> h.data.get_compression_type()
'ragged contiguous'
>>> h.data[1, 2] = -9
>>> print(h.array)
[[0.12 0.05 0.18   --   --   --   --   --   --]
 [0.05 0.11 -9.0 0.15 0.08 0.04 0.06   --   --]
 [0.15 0.19 0.15 0.17 0.07   --   --   --   --]
 [0.11 0.03 0.14 0.16 0.02 0.09 0.1  0.04 0.11]]
>>> h.data.get_compression_type()
''

Perhaps the easiest way to create a compressed field construct is to create the equivalent uncompressed field construct and then compress it with its compress method, which also compresses the metadata constructs as required.

Create a field construct and then compress it.

import numpy
import cf

# Define the array values
data = cf.Data([[280.0,   -99,   -99,   -99],
                [281.0, 279.0, 278.0, 279.5]])
data.where(cf.eq(-99), cf.masked, inplace=True)

# Create the field construct
T = cf.Field()
T.set_properties({'standard_name': 'air_temperature',
                  'units': 'K',
                  'featureType': 'timeSeries'})

# Create the domain axis constructs
X = T.set_construct(cf.DomainAxis(4))
Y = T.set_construct(cf.DomainAxis(2))

# Set the data for the field
T.set_data(data)

# Compress the data
T.compress('contiguous',
           count_properties={'long_name': 'number of obs for this timeseries'},
           inplace=True)

The new compressed field construct can now be inspected and written to a netCDF file:

Inspect the new field construct and write it to disk.

>>> T
<CF Field: air_temperature(key%domainaxis1(2), key%domainaxis0(4)) K>
>>> print(T.array)
[[280.0    --    --    --]
 [281.0 279.0 278.0 279.5]]
>>> T.data.get_compression_type()
'ragged contiguous'
>>> print(T.data.compressed_array)
[280.  281.  279.  278.  279.5]
>>> count_variable = T.data.get_count()
>>> count_variable
<CF Count: long_name=number of obs for this timeseries(2) >
>>> print(count_variable.array)
[1 4]
>>> cf.write(T, 'T_contiguous.nc')

The content of the new file is:

Inspect the new compressed dataset with the ncdump command line tool.

$ ncdump T_contiguous.nc
netcdf T_contiguous {
dimensions:
     dim = 2 ;
     element = 5 ;
variables:
     int64 count(dim) ;
             count:long_name = "number of obs for this timeseries" ;
             count:sample_dimension = "element" ;
     float air_temperature(element) ;
             air_temperature:units = "K" ;
             air_temperature:standard_name = "air_temperature" ;

// global attributes:
             :Conventions = "CF-1.7" ;
             :featureType = "timeSeries" ;
data:

 count = 1, 4 ;

 air_temperature = 280, 281, 279, 278, 279.5 ;
}

Exactly the same field construct may be also created explicitly with underlying compressed data. A construct with an underlying ragged array is created by initialising a cf.Data instance with a ragged array that is stored in one of three special array objects: RaggedContiguousArray, RaggedIndexedArray or RaggedIndexedContiguousArray.

Create a field construct explicitly with compressed data.

import numpy
import cf

# Define the ragged array values
ragged_array = cf.Data([280, 281, 279, 278, 279.5])

# Define the count array values
count_array = [1, 4]

# Create the count variable
count_variable = cf.Count(data=cf.Data(count_array))
count_variable.set_property('long_name', 'number of obs for this timeseries')

# Create the contiguous ragged array object, specifying the
# uncompressed shape
array = cf.RaggedContiguousArray(
                 compressed_array=ragged_array,
                 shape=(2, 4), size=8, ndim=2,
                 count_variable=count_variable)

# Create the field construct
T.set_properties({'standard_name': 'air_temperature',
                  'units': 'K',
                  'featureType': 'timeSeries'})

# Create the domain axis constructs for the uncompressed array
X = T.set_construct(cf.DomainAxis(4))
Y = T.set_construct(cf.DomainAxis(2))

# Set the data for the field
T.set_data(cf.Data(array))

Gathering

Compression by gathering combines axes of a multidimensional array into a new, discrete axis whilst omitting the missing values and thus reducing the number of values that need to be stored.

The list variable that is required to uncompress a gathered array is stored in a cf.List object and is retrieved with the get_list method of the cf.Data instance.

This is illustrated with the file gathered.nc (found in the sample datasets):

Inspect the compressed dataset with the ncdump command line tool.

$ ncdump -h gathered.nc
netcdf gathered {
dimensions:
     time = 2 ;
     lat = 4 ;
     lon = 5 ;
     landpoint = 7 ;
variables:
     double time(time) ;
             time:standard_name = "time" ;
             time:units = "days since 2000-1-1" ;
     double lat(lat) ;
             lat:standard_name = "latitude" ;
             lat:units = "degrees_north" ;
     double lon(lon) ;
             lon:standard_name = "longitude" ;
             lon:units = "degrees_east" ;
     int landpoint(landpoint) ;
             landpoint:compress = "lat lon" ;
     double pr(time, landpoint) ;
             pr:standard_name = "precipitation_flux" ;
             pr:units = "kg m2 s-1" ;

// global attributes:
             :Conventions = "CF-1.7" ;
}

Reading and inspecting this file shows the data presented in three-dimensional uncompressed form, whilst the underlying array is still in the two-dimensional gathered representation described in the file:

Read a field construct from a dataset that has been compressed by gathering, and inspect its data in uncompressed form.

>>> p = cf.read('gathered.nc')[0]
>>> print(p)
Field: precipitation_flux (ncvar%pr)
------------------------------------
Data            : precipitation_flux(time(2), latitude(4), longitude(5)) kg m2 s-1
Dimension coords: time(2) = [2000-02-01 00:00:00, 2000-03-01 00:00:00]
                : latitude(4) = [-90.0, ..., -75.0] degrees_north
                : longitude(5) = [0.0, ..., 40.0] degrees_east
>>> print(p.array)
[[[--       0.000122 0.0008   --       --      ]
  [0.000177 --       0.000175 0.00058  --      ]
  [--       --       --       --       --      ]
  [--       0.000206 --       0.0007   --      ]]

 [[--       0.000202 0.000174 --       --      ]
  [0.00084  --       0.000201 0.0057   --      ]
  [--       --       --       --       --      ]
  [--       0.000223 --       0.000102 --      ]]]

Inspect the underlying compressed array and the list variable that defines how to uncompress the data.

>>> p.data.get_compression_type()
'gathered'
>>> print(p.data.compressed_array)
[[0.000122 0.0008   0.000177 0.000175 0.00058 0.000206 0.0007  ]
 [0.000202 0.000174 0.00084  0.000201 0.0057  0.000223 0.000102]]
>>> list_variable = p.data.get_list()
>>> list_variable
<CF List: ncvar%landpoint(7) >
>>> print(list_variable.array)
[ 1  2  5  7  8 16 18]

Subspaces based on the uncompressed axes of the field construct are easily created:

Get subspaces based on indices of the uncompressed data.

>>> p[0]
<CF Field: precipitation_flux(time(1), latitude(4), longitude(5)) kg m2 s-1>
>>> p[1, :, 3:5]
<CF Field: precipitation_flux(time(1), latitude(4), longitude(2)) kg m2 s-1>

The underlying array of original data remains in compressed form until data array elements are modified:

Change an element of the data and show that the underlying array is no longer compressed.

>>> p.data.get_compression_type()
'gathered'
>>> p.data[1] = -9
>>> p.data.get_compression_type()
''

A construct with an underlying gathered array is created by initializing a cf.Data instance with a gathered array that is stored in the special cf.GatheredArray array object. The following code creates a simple field construct with an underlying gathered array:

Create a field construct with compressed data.

import numpy
import cf

# Define the gathered values
gathered_array = cf.Data([[2, 1, 3], [4, 0, 5]])

# Define the list array values
list_array = [1, 4, 5]

# Create the list variable
list_variable = cf.List(data=cf.Data(list_array))

# Create the gathered array object, specifying the uncompressed
# shape
array = cf.GatheredArray(
                 compressed_array=gathered_array,
                 compressed_dimension=1,
                 shape=(2, 3, 2), size=12, ndim=3,
                 list_variable=list_variable)

# Create the field construct with the domain axes and the gathered
# array
P = cf.Field(properties={'standard_name': 'precipitation_flux',
                           'units': 'kg m-2 s-1'})

# Create the domain axis constructs for the uncompressed array
T = P.set_construct(cf.DomainAxis(2))
Y = P.set_construct(cf.DomainAxis(3))
X = P.set_construct(cf.DomainAxis(2))

# Set the data for the field
P.set_data(cf.Data(array), axes=[T, Y, X])

Note that, because compression by gathering acts on a subset of the array dimensions, it is necessary to state the position of the compressed dimension in the compressed array (with the compressed_dimension parameter of the cf.GatheredArray initialisation).

The new field construct can now be inspected and written a netCDF file:

Inspect the new field construct and write it to disk.

>>> P
<CF Field: precipitation_flux(key%domainaxis0(2), key%domainaxis1(3), key%domainaxis2(2)) kg m-2 s-1>
>>> print(P.data.array)
[[[ -- 2.0]
  [ --  --]
  [1.0 3.0]]

 [[ -- 4.0]
  [ --  --]
  [0.0 5.0]]]
>>> P.data.get_compression_type()
'gathered'
>>> print(P.data.compressed_array)
[[2. 1. 3.]
 [4. 0. 5.]]
>>> list_variable = P.data.get_list()
>>> list_variable
<CF List: (3) >
>>> print(list_variable.array)
[1 4 5]
>>> cf.write(P, 'P_gathered.nc')

The content of the new file is:

Inspect new the compressed dataset with the ncdump command line tool.

$ ncdump P_gathered.nc
netcdf P_gathered {
dimensions:
     dim = 2 ;
     dim_1 = 3 ;
     dim_2 = 2 ;
     list = 3 ;
variables:
     int64 list(list) ;
             list:compress = "dim_1 dim_2" ;
     float precipitation_flux(dim, list) ;
             precipitation_flux:units = "kg m-2 s-1" ;
             precipitation_flux:standard_name = "precipitation_flux" ;

// global attributes:
             :Conventions = "CF-1.7" ;
data:

 list = 1, 4, 5 ;

 precipitation_flux =
  2, 1, 3,
  4, 0, 5 ;
}

---

PP and UM fields files

The cf.read function can read PP files and UM fields files (as output by some versions of the Unified Model, for example), mapping their contents into field constructs. 32-bit and 64-bit PP and UM fields files of any endian-ness can be read. In nearly all cases the file format is auto-detectable from the first 64 bits in the file, but for the few occasions when this is not possible 2, the um keyword of cf.read allows the format to be specified. The the UM version (if not inferable from the PP or lookup header information) and the height of the upper bound of the top model level may also be set with the um keyword.

Note that 2-d “slices” within a single file are always combined, where possible, into field constructs with 3-d, 4-d or 5-d data. This is done prior to the field construct aggregation carried out by the cf.read function.

Read a PP file into field constructs.

>>> pp = cf.read('umfile.pp')
>>> pp
[<CF Field: surface_air_pressure(time(3), latitude(73), longitude(96)) Pa>]
>>> print(pp[0])
Field: surface_air_pressure (ncvar%UM_m01s00i001_vn405)
-------------------------------------------------------
Data            : surface_air_pressure(time(3), latitude(73), longitude(96)) Pa
Cell methods    : time(3): mean
Dimension coords: time(3) = [2160-06-01 00:00:00, 2161-06-01 00:00:00, 2162-06-01 00:00:00] 360_day
                : latitude(73) = [90.0, ..., -90.0] degrees_north
                : longitude(96) = [0.0, ..., 356.25] degrees_east

Converting PP and UM fields files to netCDF files

PP and UM fields files may read with cf.read and subsequently written to disk as netCDF files with cf.write.

Write the field constructs from a PP file to a netCDF dataset.

>>> cf.write(pp, 'umfile1.nc')

Alternatively, the cfa command line tool may be used with PP and UM fields files in exactly the same way as netCDF files. This provides a view of PP and UM fields files as CF field constructs, and also easily converts PP and UM fields files to netCDF datasets on disk.

Use the ‘cfa’ shell command to view a PP file and convert it to a netCDF dataset.

$ cfa umfile.pp
CF Field: surface_air_pressure(time(3), latitude(73), longitude(96)) Pa
$ cfa -o umfile2.nc umfile.pp
$ cfa umfile2.nc
CF Field: surface_air_pressure(time(3), latitude(73), longitude(96)) Pa

Mapping of PP header items to field constructs

In addition to the creation of any CF constructs and properties that are implied by the PP and lookup header, certain lookup header items are stored, for convenience, as field construct properties:

Header item	Description	Field construct property
LBEXP	Experiment identity	runid
LBTIM	Time indicator	lbtim
LBPROC	Processing code	lbproc
LBUSER(4)	STASH code	stash_code
LBUSER(7)	Internal submodel	submodel

All such field construct properties are stored as strings. The value of LBEXP is an integer that is decoded to a string identity before being stored as a field construct property.

STASH code to standard name mappings

The standard name and units properties of a field construct are inferred from the STASH code of the PP and lookup headers. The text database that maps header items to standard names and units is stored in the file etc/STASH_to_CF.txt within the cf library installation. The database is available as a dictionary, keyed by submodel and stash code tuples. The database contains many STASH codes without standard names nor units, and will not contain user-defined STASH codes. However, modifying existing entries, or adding new ones, is straight forward with the cf.load_stash2standard_name function.

Inspect the STASH to standard name database, and modify it.

>>> type(cf.read_write.um.umread.stash2standard_name)
<class 'dict'>
>>> cf.read_write.um.umread.stash2standard_name[(1, 4)]
(['THETA AFTER TIMESTEP                ',
  'K',
  None,
  None,
  'air_potential_temperature',
  {},
  ''],)
>>> cf.read_write.um.umread.stash2standard_name[(1, 2)]
(['U COMPNT OF WIND AFTER TIMESTEP     ',
  'm s-1',
  None,
  None,
  'eastward_wind',
  {},
  'true_latitude_longitude'],
 ['U COMPNT OF WIND AFTER TIMESTEP     ',
  'm s-1',
  None,
  None,
  'x_wind',
  {},
  'rotated_latitude_longitude'])
>>> cf.read_write.um.umread.stash2standard_name[(1, 7)]
(['UNFILTERED OROGRAPHY                ',
  None,
  708.0,
  None,
  '',
  {},
 ''],)
>>> (1, 999) in cf.read_write.um.umread.stash2standard_name
False
>>> with open('new_STASH.txt', 'w') as new:
...     new.write('1!999!My STASH code!1!!!ultraviolet_index!!')
...
>>> _ = cf.load_stash2standard_name('new_STASH.txt', merge=True)
>>> cf.read_write.um.umread.stash2standard_name[(1, 999)]
(['My STASH code',
  '1',
  None,
  None,
  'ultraviolet_index',
  {},
  ''],)

---

Statistical collapses

Collapsing one or more dimensions reduces their size and replaces the data along those axes with representative statistical values. The result is a new field construct with consistent metadata for the collapsed values. Collapses are carried with the collapse method of the field construct.

By default all axes with size greater than 1 are collapsed completely (i.e. to size 1) with a given collapse method.

Find the minimum of the entire data.

>>> a = cf.read('timeseries.nc')[0]
>>> print(a)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(5), longitude(8)) K
Cell methods    : area: mean
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> b = a.collapse('minimum')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(1), latitude(1), longitude(1)) K
Cell methods    : area: mean time(1): latitude(1): longitude(1): minimum
Dimension coords: time(1) = [1964-11-30 12:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(b.array)
[[[198.9]]]

In the above example, note that the operation has been recorded in a new cell method construct (time(1): latitude(1): longitude(1): minimum) in the output field construct, and the dimension coordinate constructs each now have a single cell. The air pressure time dimension was not included in the collapse because it already had size 1 in the original field construct.

The collapse can also be applied to any subset of the field construct’s dimensions. In this case, the domain axis and coordinate constructs for the non-collapsed dimensions remain the same. This is implemented either with the axes keyword, or with a CF-netCDF cell methods-like syntax for describing both the collapse dimensions and the collapse method in a single string. The latter syntax uses construct identities instead of netCDF dimension names to identify the collapse axes.

Statistics may be created to represent variation over one dimension or a combination of dimensions.

Two equivalent techniques for creating a field construct of temporal maxima at each horizontal location.

>>> b = a.collapse('maximum', axes='T')
>>> b = a.collapse('T: maximum')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(1), latitude(5), longitude(8)) K
Cell methods    : area: mean time(1): maximum
Dimension coords: time(1) = [1964-11-30 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(b.array)
[[[310.6 309.1 309.9 311.2 310.4 310.1 310.7 309.6]
  [310.  310.7 311.1 311.3 310.9 311.2 310.6 310. ]
  [308.9 309.8 311.2 311.2 311.2 309.3 311.1 310.7]
  [310.1 310.3 308.8 311.1 310.  311.3 311.2 309.7]
  [310.9 307.9 310.3 310.4 310.8 310.9 311.3 309.3]]]

Find the horizontal maximum, with two equivalent techniques.

>>> b = a.collapse('maximum', axes=['X', 'Y'])
>>> b = a.collapse('X: Y: maximum')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(1), longitude(1)) K
Cell methods    : area: mean latitude(1): longitude(1): maximum
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : air_pressure(1) = [850.0] hPa

Variation over horizontal area may also be specified by the special identity 'area'. This may be used for any horizontal coordinate reference system.

Find the horizontal maximum using the special identity ‘area’.

>>> b = a.collapse('area: maximum')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(1), longitude(1)) K
Cell methods    : area: mean area: maximum
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : air_pressure(1) = [850.0] hPa

Collapse methods

The following collapse methods are available, over any subset of the domain axes. The “Cell method” column in the table gives the method of the new cell method construct (if one is created).

Method	Description	Cell method
'maximum'	The maximum of the values.	maximum
'minimum'	The minimum of the values.	minimum
'maximum_absolute_value'	The maximum of the absolute values.	maximum_absolute_value
'minimum_absolute_value'	The minimum of the absolute values.	minimum_absolute_value
'mid_range'	The average of the maximum and the minimum of the values.	mid_range
'range'	The absolute difference between the maximum and the minimum of the values.	range
'median'	The median of the values.	median
'sample_size'	The sample size, \(N\), as would be used for other calculations, i.e. the number of non-missing values.	point
'sum_of_weights'	The sum of \(N\) weights \(w_i\), as would be used for other calculations, is \[V_{1}=\sum_{i=1}^{N} w_i\]	sum
'sum_of_weights2'	The sum of the squares of \(N\) weights \(w_i\), as would be used for other calculations, is \[V_{2}=\sum_{i=1}^{N} w_i^{2}\]	sum
'sum'	The unweighted sum of \(N\) values \(x_i\) is \[t=\sum_{i=1}^{N} x_i\]	sum
'sum_of_squares'	The unweighted sum of the squares of \(N\) values \(x_i\) is \[t_2=\sum_{i=1}^{N} x_{i}^{2}\]	sum_of_squares
'integral'	The integral of \(N\) values \(x_i\) with corresponding cell measures \(m_i\) is \[i=\sum_{i=1}^{N} m_i x_i\] Note that the integral differs from a weighted sum in that the units of the cell measures are incorporated into the result.	sum
'mean'	The unweighted mean of \(N\) values \(x_i\) is \[\mu=\frac{1}{N}\sum_{i=1}^{N} x_i\] The weighted mean of \(N\) values \(x_i\) with corresponding weights \(w_i\) is \[\hat{\mu}=\frac{1}{V_{1}} \sum_{i=1}^{N} w_i x_i\]	mean
'mean_absolute_value'	The unweighted mean of \(N\) values \(x_i\) absoluted is \[\mu_{abs}=\frac{1}{N} \sum_{i=1}^{N}|x_i|\] The weighted mean of \(N\) values \(x_i\) absoluted with corresponding weights \(w_i\) is \[\hat{\mu}_{abs}= \frac{1}{V_{1}} \sum_{i=1}^{N} w_i |x_i|\]	mean_absolute_value
'mean_of_upper_decile'	The weighted or unweighted mean of the upper group of data values defined by the upper tenth of their distribution	mean_of_upper_decile
'variance'	The unweighted variance of \(N\) values \(x_i\) and with \(N-ddof\) degrees of freedom (\(ddof\ge0\)) is \[s_{N-ddof}^{2}= \frac{1}{N-ddof} \sum_{i=1}^{N} (x_i - \mu)^2\] The unweighted biased estimate of the variance (\(s_{N}^{2}\)) is given by \(ddof=0\) and the unweighted unbiased estimate of the variance using Bessel’s correction (\(s^{2}=s_{N-1}^{2}\)) is given by \(ddof=1\). The weighted biased estimate of the variance of \(N\) values \(x_i\) with corresponding weights \(w_i\) is \[\hat{s}_{N}^{2}= \frac{1}{V_{1}} \sum_{i=1}^{N} w_i(x_i - \hat{\mu})^{2}\] The corresponding weighted unbiased estimate of the variance is \[\hat{s}^{2}=\frac{1}{V_{1} - (V_{1}/V_{2})} \sum_{i=1}^{N} w_i(x_i - \hat{\mu})^{2}\] In both cases, the weights are assumed to be non-random reliability weights, as opposed to frequency weights.	variance
'standard_deviation'	The standard deviation is the square root of the unweighted or weighted variance, as defined in this table.	standard_deviation
'root_mean_square'	The unweighted root mean square of \(N\) values \(x_i\) is \[RMS=\sqrt{\frac{1}{N} \sum_{i=1}^{N} x_{i}^2}\] The weighted root mean square of \(N\) values \(x_i\) with corresponding weights \(w_i\) is \[\hat{RMS}=\sqrt{ \frac{1}{V_{1}} \sum_{i=1}^{N} w_i x_{i}^2}\]	root_mean_square

Data type and missing data

In all collapses, missing data array elements are accounted for in the calculation.

Any collapse method that involves a calculation (such as calculating a mean), as opposed to just selecting a value (such as finding a maximum), will return a field containing double precision floating point numbers. If this is not desired then the data type can be reset after the collapse with the dtype attribute of the field construct.

Collapse weights

For weights to be incorporated in the collapse, the axes to be weighted must be identified with the weights keyword. A collapse by a particular method is either never weighted, or may be weighted, or is always weighted, as described in the following table:

Method	Description	Weighted
'maximum'	The maximum of the values.	Never
'minimum'	The minimum of the values.	Never
'maximum_absolute_value'	The maximum of the absolute.	Never
'minimum_absolute_value'	The minimum of the absolute.	Never
'mid_range'	The average of the maximum and the minimum of the values.	Never
'range'	The absolute difference between the maximum and the minimum of the values.	Never
'median'	The median of the values.	Never
'sum'	The sum of the values.	Never
'sum_of_squares'	The sum of the squares of values.	Never
'sample_size'	The sample size, i.e. the number of non-missing values.	Never
'sum_of_weights'	The sum of weights, as would be used for other calculations.	Never
'sum_of_weights2'	The sum of squares of weights, as would be used for other calculations.	Never
'mean'	The weighted or unweighted mean of the values.	May be
'mean_absolute_value'	The mean of the absolute values.	May be
'mean_of_upper_decile'	The mean of the upper group of data values defined by the upper tenth of their distribution.	May be
'variance'	The weighted or unweighted variance of the values, with a given number of degrees of freedom.	May be
'standard_deviation'	The weighted or unweighted standard deviation of the values with a given number of degrees of freedom.	May be
'root_mean_square'	The square root of the weighted or unweighted mean of the squares of the values.	May be
'integral'	The integral of values.	Always

• Collapse methods that are “Never” weighted ignore the weights parameter, even if it is set.

• Collapse methods that “May be” weighted will only be weighted if the weights parameter is set.

• Collapse methods that are “Always” weighted require the weights parameter to be set.

Weights are either derived from the field construct’s metadata (such as cell sizes), or may be provided explicitly in the form of other field constructs containing data of weights values. In either case, the weights actually used are those derived by the weights method of the field construct called with the same weights keyword value. Collapsed axes that are not identified by the weights keyword are unweighted during the collapse operation.

Create a weighted time average.

>>> b = a.collapse('T: mean', weights='T')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(1), latitude(5), longitude(8)) K
Cell methods    : area: mean time(1): mean
Dimension coords: time(1) = [1964-11-30 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print (b.array)
[[[254.03120723 255.89723515 253.06490556 254.17815494 255.18458801 253.3684369  253.26624692 253.63818779]
  [248.92058582 253.99597591 259.67957843 257.08967972 252.57333698 252.5746236  258.90938954 253.86939502]
  [255.94716671 254.77330961 254.35929373 257.91478237 251.87670408 252.72723789 257.26038872 258.19698878]
  [258.08639474 254.8087873  254.9881741  250.98064604 255.3513003  256.66337257 257.86895702 259.49299206]
  [263.80016425 253.35825349 257.8026006  254.3173556  252.2061867  251.74150014 255.60930742 255.06260608]]]

To inspect the weights, call the weights method directly.

Create and view weights derived from the field construct’s time axis.

>>> w = a.weights(weights='T')
>>> print(w)
Field: long_name=weights (ncvar%air_potential_temperature)
----------------------------------------------------------
Data            : long_name=weights(time(120)) d
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
>>> print(w.array)
[31. 31. 29. 31. 30. 31. 30. 31. 31. 30. 31. 30. 31. 31. 28. 31. 30. 31.
 30. 31. 31. 30. 31. 30. 31. 31. 28. 31. 30. 31. 30. 31. 31. 30. 31. 30.
 31. 31. 28. 31. 30. 31. 30. 31. 31. 30. 31. 30. 31. 31. 29. 31. 30. 31.
 30. 31. 31. 30. 31. 30. 31. 31. 28. 31. 30. 31. 30. 31. 31. 30. 31. 30.
 31. 31. 28. 31. 30. 31. 30. 31. 31. 30. 31. 30. 31. 31. 28. 31. 30. 31.
 30. 31. 31. 30. 31. 30. 31. 31. 29. 31. 30. 31. 30. 31. 31. 30. 31. 30.
 31. 31. 28. 31. 30. 31. 30. 31. 31. 30. 31. 30.]

Calculate the mean over the time and latitude axes, with weights only applied to the latitude axis.

>>> b = a.collapse('T: Y: mean', weights='Y')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(1), latitude(1), longitude(8)) K
Cell methods    : area: mean time(1): latitude(1): mean
Dimension coords: time(1) = [1964-11-30 12:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print (b.array)
[[[256.15819444 254.625      255.73666667 255.43041667 253.19444444 253.31277778 256.68236111 256.42055556]]]

Specifying weighting by horizontal cell area may also use the special 'area' syntax.

Alternative syntax for specifying area weights.

>>> b = a.collapse('area: mean', weights='area')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(1), longitude(1)) K
Cell methods    : area: mean area: mean
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : air_pressure(1) = [850.0] hPa

An alternative technique for specifying weights is to set the weights keyword to the output of a call to the weights method.

Alternative syntax for specifying weights.

>>> b = a.collapse('area: mean', weights=a.weights('area'))
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(1), longitude(1)) K
Cell methods    : area: mean area: mean
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : air_pressure(1) = [850.0] hPa

See the weights method for full details on how weights may be specified.

Multiple collapses

Multiple collapses normally require multiple calls to collapse: one on the original field construct and then one on each interim field construct.

Calculate the temporal maximum of the weighted areal means using two independent calls.

>>> b = a.collapse('area: mean', weights='area').collapse('T: maximum')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(1), latitude(1), longitude(1)) K
Cell methods    : area: mean latitude(1): longitude(1): mean time(1): maximum
Dimension coords: time(1) = [1964-11-30 12:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(b.array)
[[[271.77199724]]]

If preferred, multiple collapses may be carried out in a single call to collapse by using the CF-netCDF cell methods-like syntax (note that the colon (:) is only used after the construct identity that specifies each axis, and a space delimits the separate collapses).

Calculate the temporal maximum of the weighted areal means in a single call, using the cf-netCDF cell methods-like syntax.

>>> b = a.collapse('area: mean T: maximum', weights='area')
>>> print(b.array)
[[[271.77199724]]]

Grouped collapses

A grouped collapse is one for which an axis is not collapsed completely to size 1. Instead the collapse axis is partitioned into groups and each group is collapsed to size 1. The resulting axis will generally have more than one element. For example, creating 12 annual means from a timeseries of 120 months would be a grouped collapse. The groups do not need to be created from adjacent cells, as would be the case when creating 12 multi-annual monthly means from a timeseries of 120 months.

The group keyword of collapse defines the size of the groups. Groups can be defined in a variety of ways, including with cf.Query, cf.TimeDuration (see the Time duration section) and cf.Data instances.

An element of the collapse axis can not be a member of more than one group, and may be a member of no groups. Elements that are not selected by the group keyword are excluded from the result.

Create annual maxima from a time series, defining a year to start on 1st January.

>>> y = cf.Y(month=12)
>>> y
<CF TimeDuration: P1Y (Y-12-01 00:00:00)>
>>> b = a.collapse('T: maximum', group=y)
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(10), latitude(5), longitude(8)) K
Cell methods    : area: mean time(10): maximum
Dimension coords: time(10) = [1960-06-01 00:00:00, ..., 1969-06-01 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa

Find the maximum of each group of 6 elements along an axis.

>>> b = a.collapse('T: maximum', group=6)
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(20), latitude(5), longitude(8)) K
Cell methods    : area: mean time(20): maximum
Dimension coords: time(20) = [1960-03-01 12:00:00, ..., 1969-08-31 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa

Create December, January, February maxima from a time series.

>>> b = a.collapse('T: maximum', group=cf.djf())
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(10), latitude(5), longitude(8)) K
Cell methods    : area: mean time(10): maximum time(10): maximum
Dimension coords: time(10) = [1960-01-15 12:00:00, ..., 1969-01-15 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa

Create maxima for each 3-month season of a timeseries (DJF, MAM, JJA, SON).

>>> c = cf.seasons()
>>> c
[<CF Query: month[(ge 12) | (le 2)]>
 <CF Query: month(wi (3, 5))>,
 <CF Query: month(wi (6, 8))>,
 <CF Query: month(wi (9, 11))>]
>>> b = a.collapse('T: maximum', group=c)
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(40), latitude(5), longitude(8)) K
Cell methods    : area: mean time(40): maximum time(40): maximum
Dimension coords: time(40) = [1960-01-15 12:00:00, ..., 1969-10-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa

Calculate zonal means for the western and eastern hemispheres.

>>> b = a.collapse('X: mean', group=cf.Data(180, 'degrees'))
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(5), longitude(2)) K
Cell methods    : area: mean longitude(2): mean longitude(2): mean
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(2) = [90.0, 270.0] degrees_east
                : air_pressure(1) = [850.0] hPa

Groups can be further described with the group_span (to include groups whose actual span is not equal to a given value) and the group_contiguous (to include non-contiguous groups, or any contiguous group containing overlapping cells) keywords of collapse.

Climatological statistics

Climatological statistics may be derived from corresponding portions of the annual cycle in a set of years (e.g. the average January temperatures in the climatology of 1961-1990, where the values are derived by averaging the 30 Januarys from the separate years); or from corresponding portions of the diurnal cycle in a set of days (e.g. the average temperatures for each hour in the day for May 1997). A diurnal climatology may also be combined with a multiannual climatology (e.g. the minimum temperature for each hour of the average day in May from a 1961-1990 climatology).

Calculation requires two or three collapses, depending on the quantity being created, all of which are grouped collapses. Each collapse method needs to indicate its climatological nature with one of the following qualifiers,

Method qualifier	Associated keyword
within years	within_years
within days	within_days
over years	over_years (optional)
over days	over_days (optional)

and the associated keyword to collapse specifies how the method is to be applied.

Calculate the multiannual average of the seasonal means.

>>> b = a.collapse('T: mean within years T: mean over years',
...                within_years=cf.seasons(), weights='T')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(4), latitude(5), longitude(8)) K
Cell methods    : area: mean time(4): mean within years time(4): mean over years
Dimension coords: time(4) = [1960-01-15 12:00:00, ..., 1960-10-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(b.coordinate('T').bounds.datetime_array)
[[cftime.DatetimeGregorian(1959-12-01 00:00:00) cftime.DatetimeGregorian(1969-03-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-03-01 00:00:00) cftime.DatetimeGregorian(1969-06-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-06-01 00:00:00) cftime.DatetimeGregorian(1969-09-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-09-01 00:00:00) cftime.DatetimeGregorian(1969-12-01 00:00:00)]]

Calculate the multiannual variance of the seasonal minima. Note that the units of the result have been changed from ‘K’ to ‘K2’.

>>> b = a.collapse('T: minimum within years T: variance over years',
...                within_years=cf.seasons(), weights='T')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(4), latitude(5), longitude(8)) K2
Cell methods    : area: mean time(4): minimum within years time(4): variance over years
Dimension coords: time(4) = [1960-01-15 12:00:00, ..., 1960-10-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(b.coordinate('T').bounds.datetime_array)
[[cftime.DatetimeGregorian(1959-12-01 00:00:00) cftime.DatetimeGregorian(1969-03-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-03-01 00:00:00) cftime.DatetimeGregorian(1969-06-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-06-01 00:00:00) cftime.DatetimeGregorian(1969-09-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-09-01 00:00:00) cftime.DatetimeGregorian(1969-12-01 00:00:00)]]

When collapsing over years, it is assumed by default that the each portion of the annual cycle is collapsed over all years that are present. This is the case in the above two examples. It is possible, however, to restrict the years to be included, or group them into chunks, with the over_years keyword to collapse.

Calculate the multiannual average of the seasonal means in 5 year chunks.

>>> b = a.collapse('T: mean within years T: mean over years', weights='T',
...                within_years=cf.seasons(), over_years=cf.Y(5))
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(8), latitude(5), longitude(8)) K
Cell methods    : area: mean time(8): mean within years time(8): mean over years
Dimension coords: time(8) = [1960-01-15 12:00:00, ..., 1965-10-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(b.coordinate('T').bounds.datetime_array)
[[cftime.DatetimeGregorian(1959-12-01 00:00:00) cftime.DatetimeGregorian(1964-03-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-03-01 00:00:00) cftime.DatetimeGregorian(1964-06-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-06-01 00:00:00) cftime.DatetimeGregorian(1964-09-01 00:00:00)]
 [cftime.DatetimeGregorian(1960-09-01 00:00:00) cftime.DatetimeGregorian(1964-12-01 00:00:00)]
 [cftime.DatetimeGregorian(1964-12-01 00:00:00) cftime.DatetimeGregorian(1969-03-01 00:00:00)]
 [cftime.DatetimeGregorian(1965-03-01 00:00:00) cftime.DatetimeGregorian(1969-06-01 00:00:00)]
 [cftime.DatetimeGregorian(1965-06-01 00:00:00) cftime.DatetimeGregorian(1969-09-01 00:00:00)]
 [cftime.DatetimeGregorian(1965-09-01 00:00:00) cftime.DatetimeGregorian(1969-12-01 00:00:00)]]

Calculate the multiannual average of the seasonal means, restricting the years from 1963 to 1968.

>>> b = a.collapse('T: mean within years T: mean over years', weights='T',
...                within_years=cf.seasons(), over_years=cf.year(cf.wi(1963, 1968)))
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(4), latitude(5), longitude(8)) K
Cell methods    : area: mean time(4): mean within years time(4): mean over years
Dimension coords: time(4) = [1963-01-15 00:00:00, ..., 1963-10-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(b.coordinate('T').bounds.datetime_array)
[[cftime.DatetimeGregorian(1962-12-01 00:00:00) cftime.DatetimeGregorian(1968-03-01 00:00:00)]
 [cftime.DatetimeGregorian(1963-03-01 00:00:00) cftime.DatetimeGregorian(1968-06-01 00:00:00)]
 [cftime.DatetimeGregorian(1963-06-01 00:00:00) cftime.DatetimeGregorian(1968-09-01 00:00:00)]
 [cftime.DatetimeGregorian(1963-09-01 00:00:00) cftime.DatetimeGregorian(1968-12-01 00:00:00)]]

Similarly for collapses over days, it is assumed by default that the each portion of the diurnal cycle is collapsed over all days that are present, But it is possible to restrict the days to be included, or group them into chunks, with the over_days keyword to collapse.

The calculation can be done with multiple collapse calls, which can be useful if the interim stages are needed independently, but be aware that the interim field constructs will have non-CF-compliant cell method constructs.

Calculate the multiannual maximum of the seasonal standard deviations with two separate collapse calls.

>>> b = a.collapse('T: standard_deviation within years',
...                within_years=cf.seasons(), weights='T')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(40), latitude(5), longitude(8)) K
Cell methods    : area: mean time(40): standard_deviation within years
Dimension coords: time(40) = [1960-01-15 12:00:00, ..., 1969-10-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> c = b.collapse('T: maximum over years')
>>> print(c)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(4), latitude(5), longitude(8)) K
Cell methods    : area: mean time(4): standard_deviation within years time(4): maximum over years
Dimension coords: time(4) = [1960-01-15 12:00:00, ..., 1960-10-16 12:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa

---

Other statistical operations

Cumulative sums

The cumsum method of the field construct calculates the cumulative sum of elements along a given axis. The cell bounds of the axis are updated to describe the ranges over which the sums apply, and a new sum cell method construct is added to the resulting field construct.

Calculate cumulative sums along the “T” axis, showing the cell bounds before and after the operation.

>>> a = cf.read('timeseries.nc')[0]
>>> print(a)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(5), longitude(8)) K
Cell methods    : area: mean
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> b = a.cumsum('T')
>>> print(b)
Field: air_potential_temperature (ncvar%air_potential_temperature)
------------------------------------------------------------------
Data            : air_potential_temperature(time(120), latitude(5), longitude(8)) K
Cell methods    : area: mean time(120): sum
Dimension coords: time(120) = [1959-12-16 12:00:00, ..., 1969-11-16 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : air_pressure(1) = [850.0] hPa
>>> print(a.coordinate('T').bounds[-1].dtarray)
[[cftime.DatetimeGregorian(1969-11-01 00:00:00)
  cftime.DatetimeGregorian(1969-12-01 00:00:00))]]
>>> print(b.coordinate('T').bounds[-1].dtarray)
[[cftime.DatetimeGregorian(1959-11-01 00:00:00)
  cftime.DatetimeGregorian(1969-12-01 00:00:00))]]

The treatment of missing values can be specified, as well as the positioning of coordinate values in the summed axis of the returned field construct.

Histograms

The cf.histogram function is used to record the distribution of a set of variables in the form of an N-dimensional histogram.

Each dimension of the histogram is defined by a field construct returned by the digitize method of a field construct. This “digitized” field construct defines a sequence of bins and provides indices to the bins that each value of one of the variables belongs.

Create a one-dimensional histogram of a field construct based on 10 equally-sized bins that exactly span the data range.

>>> q, t = cf.read('file.nc')
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(q.array)
[[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
 [0.023 0.036 0.045 0.062 0.046 0.073 0.006 0.066]
 [0.11  0.131 0.124 0.146 0.087 0.103 0.057 0.011]
 [0.029 0.059 0.039 0.07  0.058 0.072 0.009 0.017]
 [0.006 0.036 0.019 0.035 0.018 0.037 0.034 0.013]]
>>> indices, bins = q.digitize(10, return_bins=True)
>>> print(indices)
Field: long_name=Bin index to which each 'specific_humidity' value belongs (ncvar%q)
------------------------------------------------------------------------------------
Data            : long_name=Bin index to which each 'specific_humidity' value belongs(latitude(5), longitude(8))
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_eastg
                : time(1) = [2019-01-01 00:00:00]
>>> print(indices.array)
[[0 2 0 0 1 2 1 1]
 [1 2 2 4 3 4 0 4]
 [7 8 8 9 5 6 3 0]
 [1 3 2 4 3 4 0 0]
 [0 2 1 2 1 2 2 0]]
>>> print(bins.array)
[[0.003  0.0173]
 [0.0173 0.0316]
 [0.0316 0.0459]
 [0.0459 0.0602]
 [0.0602 0.0745]
 [0.0745 0.0888]
 [0.0888 0.1031]
 [0.1031 0.1174]
 [0.1174 0.1317]
 [0.1317 0.146 ]]
>>> h = cf.histogram(indices)
>>> print(h)
Field: number_of_observations
-----------------------------
Data            : number_of_observations(specific_humidity(10)) 1
Cell methods    : latitude: longitude: point
Dimension coords: specific_humidity(10) = [10.15, ..., 138.85000000000002] 1
>>> print(h.array)
[9 7 9 4 5 1 1 1 2 1]
>>> print(h.coordinate('specific_humidity').bounds.array)
[[0.003  0.0173]
 [0.0173 0.0316]
 [0.0316 0.0459]
 [0.0459 0.0602]
 [0.0602 0.0745]
 [0.0745 0.0888]
 [0.0888 0.1031]
 [0.1031 0.1174]
 [0.1174 0.1317]
 [0.1317 0.146 ]]

Create a two-dimensional histogram based on specific humidity and temperature bins. The temperature bins in this example are derived from a dummy temperature field construct with the same shape as the specific humidity field construct already in use.

>>> g = q.copy()
>>> g.standard_name = 'air_temperature'
>>> import numpy
>>> g[...] = numpy.random.normal(loc=290, scale=10, size=40).reshape(5, 8)
>>> g.override_units('K', inplace=True)
>>> print(g)
Field: air_temperature (ncvar%q)
--------------------------------
Data            : air_temperature(latitude(5), longitude(8)) K
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> indices_t = g.digitize(5)
>>> h = cf.histogram(indices, indices_t)
>>> print(h)
Field: number_of_observations
-----------------------------
Data            : number_of_observations(air_temperature(5), specific_humidity(10)) 1
Cell methods    : latitude: longitude: point
Dimension coords: air_temperature(5) = [281.1054839143287, ..., 313.9741786365939] K
                : specific_humidity(10) = [0.01015, ..., 0.13885] 1
>>> print(h.array)
[[2  1  5  3  2 -- -- -- -- --]
 [1  1  2 --  1 --  1  1 -- --]
 [4  4  2  1  1  1 -- --  1  1]
 [1  1 -- --  1 -- -- --  1 --]
 [1 -- -- -- -- -- -- -- -- --]]
>>> h.sum()
<CF Data(): 40 1>

Binning operations

The bin method of the field construct groups its data into bins, where each group is defined by the elements that correspond to an N-dimensional histogram bin of another set of variables, and collapses the elements in each group to a single representative value. The same collapse methods and weighting options as the collapse method are available.

The result of the binning operation is a field construct whose domain axis and dimension coordinate constructs describe the sizes of the N-dimensional bins of the other set of variables.

Find the range of values that lie in each of bin 10 equally-sized bins of the data itself.

>>> q, t = cf.read('file.nc')
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 0.001 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(q.array)
[[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
 [0.023 0.036 0.045 0.062 0.046 0.073 0.006 0.066]
 [0.11  0.131 0.124 0.146 0.087 0.103 0.057 0.011]
 [0.029 0.059 0.039 0.07  0.058 0.072 0.009 0.017]
 [0.006 0.036 0.019 0.035 0.018 0.037 0.034 0.013]]
>>> indices = q.digitize(5)
>>> b = q.bin('range', digitized=indices)
>>> print(b)
Field: specific_humidity
------------------------
Data            : specific_humidity(specific_humidity(5)) 1
Cell methods    : latitude: longitude: range
Dimension coords: specific_humidity(5) = [0.0173, ..., 0.1317] 1
>>> print(b.array)
[0.026 0.025 0.025 0.007 0.022]
>>> print(b.coordinate('specific_humidity').bounds.array)
[[0.003  0.0316]
 [0.0316 0.0602]
 [0.0602 0.0888]
 [0.0888 0.1174]
 [0.1174 0.146 ]]

Find the area-weighted mean of specific humidity values that correspond to two-dimensional bins defined by temperature and pressure values.

>>> p, t = cf.read('file2.nc')
>>> print(t)
Field: air_temperature (ncvar%t)
--------------------------------
Data            : air_temperature(latitude(5), longitude(8)) degreesC
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(p)
Field: air_pressure (ncvar%p)
-----------------------------
Data            : air_pressure(latitude(5), longitude(8)) hPa
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> t_indices = t.digitize(4)
>>> p_indices = p.digitize(6)
>>> b = q.bin('mean', digitized=[t_indices, p_indices], weights='area')
>>> print(b)
Field: specific_humidity
------------------------
Data            : specific_humidity(air_pressure(6), air_temperature(4)) 1
Cell methods    : latitude: longitude: mean
Dimension coords: air_pressure(6) = [966.6225003326126, ..., 1033.6456080043665] hPa
                : air_temperature(4) = [-12.735821567738295, ..., 9.9702610462581] degreesC
>>> print(b.array)
[[     --       --       --  0.011  ]
 [0.131    0.0145   0.0345   0.05052]
 [0.05742  0.01727  0.06392  0.0105 ]
 [     --  0.04516  0.05272  0.10194]
 [0.124    0.024    0.059    0.006  ]
 [     --  0.08971       --       --]]

Percentiles

Percentiles of the data can be computed along any subset of the axes with the percentile method of the field construct.

Find the 20th, 40th, 50th, 60th and 80th percentiles.

>>> q, t = cf.read('file.nc')
>>> print(q)
Field: specific_humidity
------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: time(1) = [2019-01-01 00:00:00]
                : latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
>>> print(q.array)
[[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
 [0.023 0.036 0.045 0.062 0.046 0.073 0.006 0.066]
 [0.11  0.131 0.124 0.146 0.087 0.103 0.057 0.011]
 [0.029 0.059 0.039 0.07  0.058 0.072 0.009 0.017]
 [0.006 0.036 0.019 0.035 0.018 0.037 0.034 0.013]]
>>> p = q.percentile([20, 40, 50, 60, 80])
>>> print(p)
Field: specific_humidity
------------------------
Data            : specific_humidity(long_name=Percentile ranks for latitude, longitude dimensions(5), latitude(1), longitude(1)) 1
Dimension coords: time(1) = [2019-01-01 00:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : long_name=Percentile ranks for latitude, longitude dimensions(5) = [20, ..., 80]
>>> print(p.array)
[[[0.0164]]
 [[0.032 ]]
 [[0.036 ]]
 [[0.0414]]
 [[0.0704]]]

Find the standard deviation of the values above the 80th percentile.

>>> p80 = q.percentile(80)
>>> print(p80)
Field: specific_humidity
------------------------
Data            : specific_humidity(latitude(1), longitude(1)) 1
Dimension coords: time(1) = [2019-01-01 00:00:00]
                : latitude(1) = [0.0] degrees_north
                : longitude(1) = [180.0] degrees_east
                : long_name=Percentile ranks for latitude, longitude dimensions(1) = [80]
>>> g = q.where(q<=p80, cf.masked)
>>> print(g.array)
[[  --    --    --    --    --    -- -- --]
 [  --    --    --    --    -- 0.073 -- --]
 [0.11 0.131 0.124 0.146 0.087 0.103 -- --]
 [  --    --    --    --    -- 0.072 -- --]
 [  --    --    --    --    --    -- -- --]]
>>> g.collapse('standard_deviation', weights='area').data
<CF Data(1, 1): [[0.024609938742357642]] 1>

Find the mean of the values above the 45th percentile along the X axis.

>>> p45 = q.percentile(45, axes='X')
>>> print(p45.array)
[[0.0189 ]
 [0.04515]
 [0.10405]
 [0.04185]
 [0.02125]]
>>> g = q.where(q<=p45, cf.masked)
>>> print(g.array)
[[  -- 0.034    --    --    -- 0.037 0.024 0.029]
 [  --    --    -- 0.062 0.046 0.073    -- 0.066]
 [0.11 0.131 0.124 0.146    --    --    --    --]
 [  -- 0.059    -- 0.07  0.058 0.072    --    --]
 [  -- 0.036    -- 0.035   --  0.037 0.034    --]]
>>> print(g.collapse('X: mean', weights='X').array)
[[0.031  ]
 [0.06175]
 [0.12775]
 [0.06475]
 [0.0355 ]]

Find the histogram bin boundaries associated with given percentiles, and digitize the data based on these bins.

>>> bins = q.percentile([0, 10, 50, 90, 100], squeeze=True)
>>> print(bins.array)
[0.003  0.0088 0.036  0.1037 0.146 ]
>>> i = q.digitize(bins, closed_ends=True)
>>> print(i.array)
[[0 1 0 1 1 2 1 1]
 [1 2 2 2 2 2 0 2]
 [3 3 3 3 2 2 2 1]
 [1 2 2 2 2 2 1 1]
 [0 2 1 1 1 2 1 1]]

---

Regridding

Regridding, also called remapping or interpolation, is the process of changing the domain of a field construct whilst preserving the qualities of the original data.

The field construct has two regridding methods: regrids for regridding data between domains with spherical coordinate systems; and regridc for regridding data between domains with Cartesian coordinate systems. The interpolation is carried by out using the ESMF package, a Python interface to the Earth System Modeling Framework regridding utility.

As with statistical collapses, regridding may be applied over a subset of the domain axes, and the domain axis constructs and coordinate constructs for the non-regridded dimensions remain the same.

Domain ancillary constructs whose data spans the regridding dimensions are also regridded, but field ancillary constructs whose data spans the regridding dimensions are removed from the regridded field construct.

Regridding methods

The following regridding methods are available (in this table, “source” and “destination” refer to the domain of the field construct being regridded, and the domain that it is being regridded to, respectively):

Method	Notes
Linear ('linear', previously called 'bilinear', which is still supported, but you are encouraged to use 'linear' instead now)	Linear interpolation in the number of dimensions corresponding to the domain. For example, for 2D domains this amounts to bilinear interpolation (that is, linear interpolation in both axes) and for regridding in 3D (only available with Cartesian-regridding) it amounts to trilinear interpolation over the three axes.
First-order conservative ('conservative' or 'conservative_1st')	Preserve the area integral of the data across the interpolation from source to destination. It uses the proportion of the area of the overlapping source and destination cells to determine appropriate weights. In particular, the weight of a source cell is the ratio of the area of intersection of the source and destination cells to the area of the whole destination cell. It does not account for the field gradient across the source cell, unlike the second-order conservative method (see below).
Second-order conservative ('conservative_2nd')	As with first-order (see above), preserves the area integral of the field between source and destination using a weighted sum, with weights based on the proportionate area of intersection. But unlike first-order, the second-order method incorporates further terms to take into consideration the gradient of the field across the source cell, thereby typically producing a smoother result of higher accuracy.
Higher order patch recovery ('patch')	A second degree polynomial regridding method, which uses a least squares algorithm to calculate the polynomial. This method gives better derivatives in the resulting destination data than the linear method.
Nearest neighbour interpolation mapping destination to nearest source ('nearest_stod')	Nearest neighbour interpolation, which is useful for extrapolation of categorical data. In this variant, each destination point is mapped to the closest source. See also below for the the other variant of the nearest neighbour approach.
Nearest neighbour interpolation mapping source to nearest destination ('nearest_dtos')	Nearest neighbour interpolation, which is useful for extrapolation of categorical data. In this variant, each source point is mapped to the closest destination. In this case, a given destination point may receive input from multiple source points, but no source point will map to more than one destination point. See also above for the other variant of nearest neighbour interpolation.

Spherical regridding

Regridding from and to spherical coordinate systems using the regrids method is only available for the ‘X’ and ‘Y’ axes simultaneously. All other axes are unchanged. The calculation of the regridding weights is based on areas and distances on the surface of the sphere, rather in Euclidean space.

The following combinations of spherical source and destination domain coordinate systems are available to the regrids method:

Spherical source domain	Spherical destination domain
Latitude-longitude	Latitude-longitude
Latitude-longitude	Rotated latitude-longitude
Latitude-longitude	Plane projection
Latitude-longitude	Tripolar
Rotated latitude-longitude	Latitude-longitude
Rotated latitude-longitude	Rotated latitude-longitude
Rotated latitude-longitude	Plane projection
Rotated latitude-longitude	Tripolar
Plane projection	Latitude-longitude
Plane projection	Rotated latitude-longitude
Plane projection	Plane projection
Plane projection	Tripolar
Tripolar	Latitude-longitude
Tripolar	Rotated latitude-longitude
Tripolar	Plane projection
Tripolar	Tripolar

The most convenient usage is when the destination domain exists in another field construct. In this case, all you need to specify is the field construct having the desired destination domain and the regridding method to use:

Regrid the field construct a conservatively onto a grid contained in field construct b.

>>> a = cf.read('air_temperature.nc')[0]
>>> b = cf.read('precipitation_flux.nc')[0]
>>> print(a)
Field: air_temperature (ncvar%tas)
----------------------------------
Data            : air_temperature(time(2), latitude(73), longitude(96)) K
Cell methods    : time(2): mean
Dimension coords: time(2) = [1860-01-16 00:00:00, 1860-02-16 00:00:00] 360_day
                : latitude(73) = [-90.0, ..., 90.0] degrees_north
                : longitude(96) = [0.0, ..., 356.25] degrees_east
                : height(1) = [2.0] m
>>> print(b)
Field: precipitation_flux (ncvar%tas)
-------------------------------------
Data            : precipitation_flux(time(1), latitude(64), longitude(128)) kg m-2 day-1
Cell methods    : time(1): mean (interval: 1.0 month)
Dimension coords: time(1) = [0450-11-16 00:00:00] noleap
                : latitude(64) = [-87.86380004882812, ..., 87.86380004882812] degrees_north
                : longitude(128) = [0.0, ..., 357.1875] degrees_east
                : height(1) = [2.0] m
>>> c = a.regrids(b, 'conservative')
>>> print(c)
Field: air_temperature (ncvar%tas)
----------------------------------
Data            : air_temperature(time(2), latitude(64), longitude(128)) K
Cell methods    : time(2): mean
Dimension coords: time(2) = [1860-01-16 00:00:00, 1860-02-16 00:00:00] 360_day
                : latitude(64) = [-87.86380004882812, ..., 87.86380004882812] degrees_north
                : longitude(128) = [0.0, ..., 357.1875] degrees_east
                : height(1) = [2.0] m

It is generally not necessary to specify which are the ‘X’ and ‘Y’ axes in the domains of both the source and destination field constructs, since they will be automatically identified by their metadata. However, in cases when this is not possible (such as for tripolar domains) the src_axes or dst_axes keywords of the regrids method can be used.

It may be that the required destination domain does not exist in a field construct. In this case, the latitude and longitudes of the destination domain may be defined solely by dimension or auxiliary coordinate constructs.

Regrid ‘a’ onto two-dimensional (curvilinear) dimension coordinates latitude and longitude.

>>> import numpy
>>> lat = cf.DimensionCoordinate(data=cf.Data(numpy.arange(-90, 92.5, 2.5), 'degrees_north'))
>>> lon = cf.DimensionCoordinate(data=cf.Data(numpy.arange(0, 360, 5.0), 'degrees_east'))
>>> c = a.regrids({'latitude': lat, 'longitude': lon}, 'linear')
Field: air_temperature (ncvar%tas)
----------------------------------
Data            : air_temperature(time(2), latitude(73), longitude(72)) K
Cell methods    : time(2): mean
Dimension coords: time(2) = [1860-01-16 00:00:00, 1860-02-16 00:00:00] 360_day
                : latitude(73) = [-90.0, ..., 90.0] degrees_north
                : longitude(72) = [0.0, ..., 355.0] degrees_east
                : height(1) = [2.0] m

A destination domain defined by two-dimensional (curvilinear) latitude and longitude auxiliary coordinate constructs can also be specified in a similar manner.

An axis is cyclic if cells at both of its ends are actually geographically adjacent. In spherical regridding, only the ‘X’ axis has the potential for being cyclic. For example, a longitude cell spanning 359 to 360 degrees east is proximate to the cell spanning 0 to 1 degrees east.

When a cyclic dimension can not be automatically detected, such as when its dimension coordinate construct does not have bounds, cyclicity may be set with the src_cyclic or dst_cyclic keywords of the regrids method.

To find out whether a dimension is cyclic use the iscyclic method of the field construct, or to manually set its cyclicity use the cyclic method. If the destination domain has been defined by a dictionary of dimension coordinate constructs, then cyclicity can be registered by setting a period of cyclicity with the period method of the dimension coordinate construct.

Cartesian regridding

Cartesian regridding with the regridc method is very similar to spherical regridding, except regridding dimensions are not restricted to the horizontal plane, the source and destination domains are assumed to be Euclidian spaces for the purpose of calculating regridding weights, and all dimensions are assumed to be non-cyclic by default.

Cartesian regridding can be done in up to three dimensions. It is often used for regridding along the time dimension. A plane projection coordinate system can be regridded with Cartesian regridding, which will produce similar results to using using spherical regridding.

Regrid the time axis ‘T’ of field ‘a’ with the linear method onto the grid specified in the dimension coordinate time.

>>> time = cf.DimensionCoordinate()
>>> time.standard_name='time'
>>> time.set_data(cf.Data(numpy.arange(0.5, 60, 1),
...                       units='days since 1860-01-01', calendar='360_day'))
>>> time
<CF DimensionCoordinate: time(60) days since 1860-01-01 360_day>
>>> c = a.regridc({'T': time}, axes='T', method='linear')
Field: air_temperature (ncvar%tas)
----------------------------------
Data            : air_temperature(time(60), latitude(73), longitude(96)) K
Cell methods    : time(60): mean
Dimension coords: time(60) = [1860-01-01 12:00:00, ..., 1860-02-30 12:00:00] 360_day
                : latitude(73) = [-90.0, ..., 90.0] degrees_north
                : longitude(96) = [0.0, ..., 356.25] degrees_east
                : height(1) = [2.0] m

Note the requirement for the conservative method of contiguous, non-overlapping bounds on the destination domain:

Regrid the time axis ‘T’ of field ‘a’ conservatively (to first order) onto the grid specified in the dimension coordinate time.

>>> c = a.regridc({'T': time}, axes='T', method='conservative')  # Raises Exception
ValueError: Destination coordinates must have contiguous, non-overlapping bounds for conservative regridding.
>>> bounds = time.create_bounds()
>>> time.set_bounds(bounds)
>>> c = a.regridc({'T': time}, axes='T', method='conservative')
>>> print(c)
Field: air_temperature (ncvar%tas)
----------------------------------
Data            : air_temperature(time(60), latitude(73), longitude(96)) K
Cell methods    : time(60): mean
Dimension coords: time(60) = [1860-01-01 12:00:00, ..., 1860-02-30 12:00:00] 360_day
                : latitude(73) = [-90.0, ..., 90.0] degrees_north
                : longitude(96) = [0.0, ..., 356.25] degrees_east
                : height(1) = [2.0] m

Cartesian regridding to the dimension of another field construct is also possible, similarly to spherical regridding.

Regridding masked data

The data mask of the source field construct is taken into account, such that the regridded data will be masked in regions where the source data is masked. By default the mask of the destination field construct is not used, but can be taken into account by setting use_dst_mask keyword to the regrids or regridc methods. For example, this is useful when part of the destination domain is not being used (such as the land portion of an ocean grid).

For conservative regridding, masking is done on cells. Masking a destination cell means that the cell won’t participate in the regridding. For all other regridding methods, masking is done on points. For these methods, masking a destination point means that the point will not participate in the regridding.

Vertical regridding

The only option for regridding along a vertical axis is to use Cartesian regridding. However, care must be taken to ensure that the vertical axis is transformed so that it’s coordinate values vary linearly. For example, to regrid data on one set of vertical pressure coordinates to another set, the pressure coordinates may first be transformed into the logarithm of pressure, and then changed back to pressure coordinates after the regridding operation.

Regrid a field construct from one set of pressure levels to another.

>>> v = cf.read('vertical.nc')[0]
>>> print(v)
Field: eastward_wind (ncvar%ua)
-------------------------------
Data            : eastward_wind(time(3), air_pressure(5), grid_latitude(11), grid_longitude(10)) m s-1
Cell methods    : time(3): mean
Dimension coords: time(3) = [1979-05-01 12:00:00, 1979-05-02 12:00:00, 1979-05-03 12:00:00] gregorian
                : air_pressure(5) = [850.0, ..., 50.0] hPa
                : grid_latitude(11) = [23.32, ..., 18.92] degrees
                : grid_longitude(10) = [-20.54, ..., -16.58] degrees
Auxiliary coords: latitude(grid_latitude(11), grid_longitude(10)) = [[67.12, ..., 66.07]] degrees_north
                : longitude(grid_latitude(11), grid_longitude(10)) = [[-45.98, ..., -31.73]] degrees_east
Coord references: grid_mapping_name:rotated_latitude_longitude
>>> z_p = v.construct('Z')
>>> print(z_p.array)
[850. 700. 500. 250.  50.]
>>> z_ln_p = z_p.log()
>>> print(z_ln_p.array)
[6.74523635 6.55108034 6.2146081  5.52146092 3.91202301]
>>> _ = v.replace_construct('Z', z_ln_p)
>>> new_z_p = cf.DimensionCoordinate(data=cf.Data([800, 705, 632, 510, 320.], 'hPa'))
>>> new_z_ln_p = new_z_p.log()
>>> new_v = v.regridc({'Z': new_z_ln_p}, axes='Z', method='linear')
>>> new_v.replace_construct('Z', new_z_p)
>>> print(new_v)
Field: eastward_wind (ncvar%ua)
-------------------------------
Data            : eastward_wind(time(3), Z(5), grid_latitude(11), grid_longitude(10)) m s-1
Cell methods    : time(3): mean
Dimension coords: time(3) = [1979-05-01 12:00:00, 1979-05-02 12:00:00, 1979-05-03 12:00:00] gregorian
                : Z(5) = [800.0, ..., 320.0] hPa
                : grid_latitude(11) = [23.32, ..., 18.92] degrees
                : grid_longitude(10) = [-20.54, ..., -16.58] degrees
Auxiliary coords: latitude(grid_latitude(11), grid_longitude(10)) = [[67.12, ..., 66.07]] degrees_north
                : longitude(grid_latitude(11), grid_longitude(10)) = [[-45.98, ..., -31.73]] degrees_east
Coord references: grid_mapping_name:rotated_latitude_longitude

Note that the replace_construct method of the field construct is used to easily replace the vertical dimension coordinate construct, without having to manually match up the corresponding domain axis construct and construct key.

---

Mathematical operations

Arithmetical operations

A field construct may be arithmetically combined with another field construct, or any other object that is broadcastable to its data. See the comprehensive list of available binary operations.

When combining with another field construct, its data is actually combined, but only after being transformed so that it is broadcastable to the first field construct’s data. This is done by using the metadata constructs of the two field constructs to create a mapping of physically compatible dimensions between the fields, and then manipulating the dimensions of the other field construct’s data to ensure that they are broadcastable.

In any case, a field construct may appear as the left or right operand, and augmented assignments are possible.

Automatic units conversions are also carried out between operands during operations, and if one operand has no units then the units of the other are assumed.

Apply some binary arithmetic operations to combine the data for a pair of field constructs.

>>> q, t = cf.read('file.nc')
>>> t.data.stats()
{'min': <CF Data(): 260.0 K>,
 'mean': <CF Data(): 269.9244444444445 K>,
 'max': <CF Data(): 280.0 K>,
 'range': <CF Data(): 20.0 K>,
 'mid_range': <CF Data(): 270.0 K>,
 'standard_deviation': <CF Data(): 5.942452002538104 K>,
 'sample_size': 90}
>>> x = t + t
>>> x
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>
>>> x.min()
<CF Data(): 520.0 K>
>>> (t - 2).min()
<CF Data(): 258.0 K>
>>> (2 + t).min()
<CF Data(): 262.0 K>
>>> (t * list(range(9))).min()
<CF Data(): 0.0 K>
>>> (t + cf.Data(numpy.arange(20, 29), '0.1 K')).min()
<CF Data(): 262.6 K>

Apply a binary addition operation to apply an offset to the units and permute the axes of air temperature data on a field construct. Note the use of augmented assignment to apply an offset to the units.

>>> u = t.copy()
>>> u.transpose(inplace=True)
>>> u.Units -= 273.15
>>> u[0]
<CF Field: air_temperature(grid_longitude(1), grid_latitude(10), atmosphere_hybrid_height_coordinate(1)) K @ 273.15>
>>> t + u[0]
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>

If the physical nature of the result differs from both operands, then the “standard_name” and “long_name” properties are removed. This is the case if the units of the result differ from both operands, or if they have different standard names.

Applying a binary operation where the resultant field construct has a different physical nature to the two operands. Note the removal of the ‘standard_name’ property to account for this.

>>> t.identities()
['air_temperature',
 'Conventions=CF-1.7',
 'project=research',
 'units=K',
 'standard_name=air_temperature',
 'ncvar%ta']
>>> u = t * cf.Data(10, 'm s-1')
>>> u.identities()
['Conventions=CF-1.7',
 'project=research',
 'units=m.s-1.K',
 'ncvar%ta']

The domain metadata constructs of the result of a successful arithmetical operation between two field constructs are unambiguously well defined: The domain metadata constructs of the result of a succesful operation are copied from the left hand side (LHS) operand, except when a coordinate construct in the LHS operand has size 1 and the corresponding coordinate construct in right hand side (RHS) field construct operand has size greater than 1. In this case the coordinate construct from the RHS operand is used in the result, to match up with the data broadcasting that will have occured during the operation.

In circumstances when domain metadata constructs in the result can not be inferred unambiguously then an exception will be raised. For example, this will be the case if both operands are field constructs with corresponding coordinate constructs of size greater than 1 and with different coordinate values. In such circumstances, the field constructs’ data instances may be operated on directly, bypassing any checks on the metadata. See Operating on the field constructs’ data for more details. (This will be made easier in a future release with a new function for combining such field constructs.)

Warning

Care must be taken when combining a field construct with a numpy array or a Data instance, due to the ways in which both of these objects allow themselves to be combined with other types:

• If the field construct is on the left hand side (LHS) of the operation then, as expected, a field construct is returned whose data is the combination of the original field construct’s data and the numpy array or Data instance on the right hand side (RHS).

• If, however, the field construct is on the RHS then a numpy array or Data instance (which ever type is on the LHS) is returned, containing the same data as in the first case.

A field construct will not be returned if the left hand operand is a numpy array or a ‘Data’ instance.

>>> import numpy
>>> q, t = cf.read('fil.nc')
>>> a = numpy.array(1000)
>>> type(t * a)
cf.field.Field
>>> type(a + t)
numpy.ndarray
>>> b = numpy.random.randn(t.size).reshape(t.shape)
>>> type(t * b)
cf.field.Field
>>> type(b * t)
numpy.ndarray
>>> type(t - cf.Data(b))
cf.field.Field
>>> type(cf.Data(b) * t)
cf.data.data.Data

Unary operations

Python unary operators also work on the field construct’s data, returning a new field construct with modified data values. See the comprehensive list of available unary operations.

Apply some unary operations to a field construct’s data.

>>> q, t = cf.read('file.nc')
>>> print(q.array)
[[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
 [0.023 0.036 0.045 0.062 0.046 0.073 0.006 0.066]
 [0.11  0.131 0.124 0.146 0.087 0.103 0.057 0.011]
 [0.029 0.059 0.039 0.07  0.058 0.072 0.009 0.017]
 [0.006 0.036 0.019 0.035 0.018 0.037 0.034 0.013]]
>>> print(-q.array)
[[-0.007 -0.034 -0.003 -0.014 -0.018 -0.037 -0.024 -0.029]
 [-0.023 -0.036 -0.045 -0.062 -0.046 -0.073 -0.006 -0.066]
 [-0.11  -0.131 -0.124 -0.146 -0.087 -0.103 -0.057 -0.011]
 [-0.029 -0.059 -0.039 -0.07  -0.058 -0.072 -0.009 -0.017]
 [-0.006 -0.036 -0.019 -0.035 -0.018 -0.037 -0.034 -0.013]]
>>> print(abs(-q).array)
[[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
 [0.023 0.036 0.045 0.062 0.046 0.073 0.006 0.066]
 [0.11  0.131 0.124 0.146 0.087 0.103 0.057 0.011]
 [0.029 0.059 0.039 0.07  0.058 0.072 0.009 0.017]
 [0.006 0.036 0.019 0.035 0.018 0.037 0.034 0.013]]

Relational operations

A field construct may compared with another field construct, or any other object that is broadcastable to its data. See the comprehensive list of available relational operations. The result is a field construct with Boolean data values.

When comparing with another field construct, its data is actually combined, but only after being transformed so that it is broadcastable to the first field construct’s data. This is done by using the metadata constructs of the two field constructs to create a mapping of physically compatible dimensions between the fields, and then manipulating the dimensions of the other field construct’s data to ensure that they are broadcastable.

In any case, a field construct may appear as the left or right operand.

Automatic units conversions are also carried out between operands during operations, and if one operand has no units then the units of the other are assumed.

Produce field constructs of Boolean data encapsulating the nature of some relations between a field construct and another operand.

>>> q, t = cf.read('file.nc')
>>> print(q.array)
[[0.007 0.034 0.003 0.014 0.018 0.037 0.024 0.029]
 [0.023 0.036 0.045 0.062 0.046 0.073 0.006 0.066]
 [0.11  0.131 0.124 0.146 0.087 0.103 0.057 0.011]
 [0.029 0.059 0.039 0.07  0.058 0.072 0.009 0.017]
 [0.006 0.036 0.019 0.035 0.018 0.037 0.034 0.013]]
>>> print((q == q).array)
[[ True  True  True  True  True  True  True  True]
 [ True  True  True  True  True  True  True  True]
 [ True  True  True  True  True  True  True  True]
 [ True  True  True  True  True  True  True  True]
 [ True  True  True  True  True  True  True  True]]
>>> print((q < 0.05).array)
[[ True  True  True  True  True  True  True  True]
 [ True  True  True False  True False  True False]
 [False False False False False False False  True]
 [ True False  True False False False  True  True]
 [ True  True  True  True  True  True  True  True]]
>>> print((q >= q[0]).array)
[[ True  True  True  True  True  True  True  True]
 [ True  True  True  True  True  True False  True]
 [ True  True  True  True  True  True  True False]
 [ True  True  True  True  True  True False False]
 [False  True  True  True  True  True  True False]]

The “standard_name” and “long_name” properties are removed from the result, which also has no units.

A field construct of Boolean data created from a relational operation on a field construct and another operand will be stripped of its standard_name property (and its long_name property if it has been set, unlike for ‘q’ here).

>>> q.identities()
['specific_humidity',
 'Conventions=CF-1.7',
 'project=research',
 'units=1',
 'standard_name=specific_humidity',
 'ncvar%q']
>>> r = q > q.mean()
>>> r.identities()
['Conventions=CF-1.7',
 'project=research',
 'units=',
 'ncvar%q']

The domain metadata constructs of the result of a successful relational operation between two field constructs are unambiguously well defined: The domain metadata constructs of the result of a succesful operation are copied from the left hand side (LHS) operand, except when a coordinate construct in the LHS operand has size 1 and the corresponding coordinate construct in right hand side (RHS) field construct operand has size greater than 1. In this case the coordinate construct from the RHS operand is used in the result, to match up with the data broadcasting that will have occured during the operation.

In circumstances when domain metadata constructs in the result can not be inferred unambiguously then an exception will be raised. For example, this will be the case if both operands are field constructs with corresponding coordinate constructs of size greater than 1 and with different coordinate values. In such circumstances, the field constructs’ data instances may be operated on directly, bypassing any checks on the metadata. See Operating on the field constructs’ data for more details. (This will be made easier in a future release with a new function for combining such field constructs.)

Arithmetical and relational operations with insufficient metadata

When both operands of an arithmetical or relational operation are field constructs then the creation of the mapping of physically compatible dimensions relies on there being sufficient metadata. By default, the mapping relies on their being “strict” identities for the metadata constucts with multi-valued data. The strict identity is restricted standard_name property (or id attribute), and may be returned by the identity method of a construct:

Find the “strict” identity of a construct.

>>> y = q.coordinate('Y')
>>> y.identity(strict=True)
'latitude'
>>> del y.standard_name
>>> y.identity(strict=True)
''

If there is insufficient metadata to create a mapping of physically compatible dimensions, then there are various techniques that allow the operation to proceed:

• Option 1: The operation may applied to the field constructs’ data instances instead. See Operating on the field constructs’ data for more details.

• Option 2: If the mapping is not possible due to the absence of standard_name properties (or id attributes) on metadata constructs that are known to correspond, then setting “relaxed identities” with the cf.RELAXED_IDENTITIES function may help. Setting relaxed identities to True allows the long_name property and netCDF variable name (see the netCDF interface), to also be considered when identifying constructs.

• Option 3: Add more metadata to the field and metadata constructs.

Operating on the field constructs’ data

Arithmetical and relational operations between may also be carried out on their data instances, thereby bypassing any reference to, or checks on, the metadata constucts. This can be useful if there insufficient metadata for determining if the two field constructs are compatible; or if the domain metadata constructs of the result can not be unambiguously defined.

In such cases the data instances may be operated on instead and the result then inserted into one of the field constructs, either with the set_data method of the field construct, or with indexed assignment. The former technique is faster and more memory efficient, but the latter technique allows broadcasting. Alternatively, for augmented assignments, the field construct data may be changed in-place.

It is up to the user to ensure that the data instances are consistent in terms of size 1 dimensions (to satisfy the numpy broadcasting rules), dimension order and dimension direction, and that the resulting data is compatible with the metadata of the field constuct which will contain it. Automatic units conversions are, however, still accounted for when combining the data instances.

Operate on the data and use ‘set_data’ to put the resulting data into the new field construct.

>>> t.min()
<CF Data(): 260.0 K>
>>> u = t.copy()
>>> new_data = t.data - t.data
>>> u.set_data(new_data)
>>> u
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>
>>> u.min()
<CF Data(): 0.0 K>

Update the data with indexed assignment

 >>> u[...] = new_data
 >>> u.min()
 <CF Data(): 0.0 K>

An example of augmented assignment involving the data of two field constructs.

>>> t.data -= t.data
>>> t.min()
<CF Data(): 0.0 K>

Trigonometrical and hyperbolic functions

The field construct and metadata constructs have methods to apply trigonometric and hyperbolic functions, and their inverses, element-wise to the data. These preserve the metadata but change the construct’s units.

The field construct and metadata constructs support the following trigonometrical methods:

Method	Description
arccos	Take the inverse trigonometric cosine of the data element-wise.
arcsin	Take the inverse trigonometric sine of the data element-wise.
arctan	Take the inverse trigonometric tangent of the data element-wise.
cos	Take the trigonometric cosine of the data element-wise.
sin	Take the trigonometric sine of the data element-wise.
tan	Take the trigonometric tangent of the data element-wise.

The field construct and metadata constructs also support the following hyperbolic methods:

Method	Description
arccosh	Take the inverse hyperbolic cosine of the data element-wise.
arcsinh	Take the inverse hyperbolic sine of the data element-wise.
arctanh	Take the inverse hyperbolic tangent of the data element-wise.
cosh	Take the hyperbolic cosine of the data element-wise.
sinh	Take the hyperbolic sine of the data element-wise.
tanh	Take the hyperbolic tangent of the data element-wise.

Find the sine of each latitude coordinate value.

>>> q, t = cf.read('file.nc')
>>> lat = q.dimension_coordinate('latitude')
>>> lat.data
<CF Data(5): [-75.0, ..., 75.0] degrees_north>
>>> sin_lat = lat.sin()
>>> sin_lat.data
<CF Data(5): [-0.9659258262890683, ..., 0.9659258262890683] 1>

The “standard_name” and “long_name” properties are removed from the result.

Note that a number of the inverse methods have mathematically restricted domains (see also here) and therefore may return “invalid” values (nan or inf). When applying these methods to constructs with masked data, you may prefer to output masked values instead of invalid ones. In this case, you can use mask_invalid to do the conversion afterwards:

Take the `arctanh` of some masked data and then transform resultant invalid values into masked data values.

>>> d = cf.Data([2, 1.5, 1, 0.5, 0], mask=[1, 0, 0, 0, 1])
>>> e = d.arctanh()
>>> print(e.array)
[-- nan inf 0.5493061443340548 --]
>>> e.mask_invalid(inplace=True)
>>> print(e.array)
[-- -- -- 0.5493061443340548 --]

Exponential and logarithmic functions

The field construct and metadata constructs have exp and log methods for applying exponential and logarithmic functions respectively element-wise to the data, preserving the metadata but changing the construct’s units where required.

Find the logarithms and exponentials of field constructs.

>>> q
<CF Field: specific_humidity(latitude(5), longitude(8)) 1>
>>> q.log()
<CF Field: specific_humidity(latitude(5), longitude(8)) ln(re 1)>
>>> q.exp()
<CF Field: specific_humidity(latitude(5), longitude(8)) 1>
>>> t
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) K>
>>> t.log(base=10)
<CF Field: air_temperature(atmosphere_hybrid_height_coordinate(1), grid_latitude(10), grid_longitude(9)) lg(re 1 K)>
>>> t.exp()  # Raises Exception
ValueError: Can't take exponential of dimensional quantities: <Units: K>

The “standard_name” and “long_name” properties are removed from the result.

Rounding and truncation

The field construct and metadata constructs the following methods to round and truncate their data:

Method	Description
ceil	The ceiling of the data, element-wise.
clip	Limit the values in the data.
floor	Floor the data array, element-wise.
rint	Round the data to the nearest integer, element-wise.
round	Round the data to the given number of decimals.
trunc	Truncate the data, element-wise.

Convolution filters

A convolution of the field construct data with a filter along a single domain axis can be calculated, which also updates the bounds of a relevant dimension coordinate construct to account for the width of the filter. Convolution filters are carried with the convolution_filter method of the field construct.

Calculate a 5-point weighted mean of the ‘X’ axis. Since the the ‘X’ axis is cyclic, the convolution wraps by default.

>>> print(q)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> q.iscyclic('X')
True
>>> r = q.convolution_filter([0.1, 0.15, 0.5, 0.15, 0.1], axis='X')
>>> print(r)
Field: specific_humidity (ncvar%q)
----------------------------------
Data            : specific_humidity(latitude(5), longitude(8)) 1
Cell methods    : area: mean
Dimension coords: latitude(5) = [-75.0, ..., 75.0] degrees_north
                : longitude(8) = [22.5, ..., 337.5] degrees_east
                : time(1) = [2019-01-01 00:00:00]
>>> print(q.dimension_coordinate('X').bounds.array)
[[  0.  45.]
 [ 45.  90.]
 [ 90. 135.]
 [135. 180.]
 [180. 225.]
 [225. 270.]
 [270. 315.]
 [315. 360.]]
>>> print(r.dimension_coordinate('X').bounds.array)
[[-90. 135.]
 [-45. 180.]
 [  0. 225.]
 [ 45. 270.]
 [ 90. 315.]
 [135. 360.]
 [180. 405.]
 [225. 450.]]

The convolution_filter method of the field construct also has options to

• Specify how the input array is extended when the filter overlaps a border, and

• Control the placement position of the filter window.

Note that the scipy.signal.windows package has suite of window functions for creating weights for filtering:

Calculate a 3-point exponential filter of the ‘Y’ axis. Since the ‘Y’ axis is not cyclic, the convolution by default inserts missing data at points for which the filter window extends beyond the array.

>>> from scipy.signal import windows
>>> exponential_weights = windows.exponential(3)
>>> print(exponential_weights)
[0.36787944 1.         0.36787944]
>>> r = q.convolution_filter(exponential_weights, axis='Y')
>>> print(r.array)
[[--      --      --      --      --      --      --      --     ]
 [0.06604 0.0967  0.09172 0.12086 0.08463 0.1245  0.0358  0.08072]
 [0.12913 0.16595 0.1549  0.19456 0.12526 0.15634 0.06252 0.04153]
 [0.07167 0.12044 0.09161 0.13659 0.09663 0.1235  0.04248 0.02583]
 [--      --      --      --      --      --      --      --     ]]

The magnitude of the integral of the filter (i.e. the sum of the weights defined by the weights parameter) affects the convolved values. For example, weights of [0.2, 0.2 0.2, 0.2, 0.2] will produce a 5-point (non-weighted) running mean; and weights of [1, 1, 1, 1, 1] will produce a 5-point running sum. Note that the weights returned by functions of the scipy.signal.windows package do not necessarily sum to 1.

Derivatives

The derivative along a dimension of the field construct’s data can be calculated as a centred finite difference with the derivative method. If the axis is cyclic then the derivative wraps around by default, otherwise it may be forced to wrap around; a one-sided difference is calculated at the edges; or missing data is inserted.

Calculate for a field construct’s data the derivative along both the ‘X’ and ‘Y’ axes, where the former (by default) uses missing values in the calculation, but the latter has been told to use a one-sided finite difference at the boundary.

>>> r = q.derivative('X')
>>> r = q.derivative('Y', one_sided_at_boundary=True)

Relative vorticity

The relative vorticity of the wind may be calculated on a global or limited area domain, and in Cartesian or spherical polar coordinate systems.

The relative vorticity of wind defined on a Cartesian domain (such as a plane projection) is defined as

\[\zeta _{cartesian} = \frac{\delta v}{\delta x} - \frac{\delta u}{\delta y}\]

where \(x\) and \(y\) are points on along the ‘X’ and ‘Y’ Cartesian dimensions respectively; and \(u\) and \(v\) denote the ‘X’ and ‘Y’ components of the horizontal winds.

If the wind field is defined on a spherical latitude-longitude domain then a correction factor is included:

\[\zeta _{spherical} = \frac{\delta v}{\delta x} - \frac{\delta u}{\delta y} + \frac{u}{r}tan(\phi)\]

where \(u\) and \(v\) denote the longitudinal and latitudinal components of the horizontal wind field; \(r\) is the radius of the Earth; and \(\phi\) is the latitude at each point.

The cf.relative_vorticity function creates a relative vorticity field construct from field constructs containing the wind components using finite differences to approximate the derivatives. Dimensions other than ‘X’ and ‘Y’ remain unchanged by the operation.

Generate a relative vorticity field construct from wind component field constructs, then round the field’s data to 8 decimal places.

>>> u, v = cf.read('wind_components.nc')
>>> zeta = cf.relative_vorticity(u, v)
>>> print(zeta)
Field: atmosphere_relative_vorticity (ncvar%va)
-----------------------------------------------
Data            : atmosphere_relative_vorticity(time(1), atmosphere_hybrid_height_coordinate(1), latitude(9), longitude(8)) s-1
Dimension coords: time(1) = [1978-09-01 06:00:00] 360_day
                : atmosphere_hybrid_height_coordinate(1) = [9.9982] m
                : latitude(9) = [-90, ..., 70] degrees_north
                : longitude(8) = [0, ..., 315] degrees_east
Coord references: standard_name:atmosphere_hybrid_height_coordinate
Domain ancils   : atmosphere_hybrid_height_coordinate(atmosphere_hybrid_height_coordinate(1)) = [9.9982] m
                : long_name=vertical coordinate formula term: b(k)(atmosphere_hybrid_height_coordinate(1)) = [0.9989]
                : surface_altitude(latitude(9), longitude(8)) = [[2816.25, ..., 2325.98]] m
>>> print(zeta.array.round(8))
[[[[--        --        --        --        --        --        --        --       ]
   [-2.04e-06  1.58e-06  5.19e-06  4.74e-06 -4.76e-06 -2.27e-06  9.55e-06 -3.64e-06]
   [-8.4e-07  -4.37e-06 -3.55e-06 -2.31e-06 -3.6e-07  -8.58e-06 -2.45e-06  6.5e-07 ]
   [ 4.08e-06  4.55e-06  2.75e-06  4.15e-06  5.16e-06  4.17e-06  4.67e-06 -7e-07   ]
   [-1.4e-07  -3.5e-07  -1.27e-06 -1.29e-06  2.01e-06  4.4e-07  -2.5e-06   2.05e-06]
   [-7.3e-07  -1.59e-06 -1.77e-06 -3.13e-06 -7.9e-07  -5.1e-07  -2.79e-06  1.12e-06]
   [-3.7e-07   7.1e-07   1.52e-06  6.5e-07  -2.75e-06 -4.3e-07   1.62e-06 -6.6e-07 ]
   [ 9.5e-07  -8e-07     6.6e-07   7.2e-07  -2.13e-06 -4.5e-07  -7.5e-07  -1.11e-06]
   [--        --        --        --        --        --        --        --       ]]]]

For axes that are not cyclic, missing data is inserted at the edges by default; otherwise it may be forced to wrap around, or a one-sided difference is calculated at the edges. If the longitudinal axis is cyclic then the derivative wraps around by default.

---

Footnotes

1

Requires the netCDF4 python package to have been built with OPeNDAP support enabled. See http://unidata.github.io/netcdf4-python for details.

2

For example, if the LBYR, LBMON, LBDAY and LBHR entries are all zero for the first header in a 32-bit PP file, the file format can not reliably be detected automatically.